WBBSE Class 9 Math Koshe Dekhi 5.2.রৈখিক সহসমীকরণ (দুই চল বিশিষ্ট )কষে দেখি ৫.২|Ganit Prakash Class 9 Koshe Dekhi 5.2 Solution|Ganit Prakash Class Nine Koshe Dekhi 5.2 Somadhan|গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.২ সমাধান|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.২ সমাধান|Linear Simultaneous Equation Chapter 5 Exercise 5.2 Solution|West Bengal Board Class 9 Math Book Solution.
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
WBBSE Class 9 Math Koshe Dekhi 5.2.রৈখিক সহসমীকরণ (দুই চল বিশিষ্ট )কষে দেখি ৫.২|Ganit Prakash Class 9 Koshe Dekhi 5.2 Solution|Ganit Prakash Class Nine Koshe Dekhi 5.2 Somadhan|গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.২ সমাধান|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.২ সমাধান|Linear Simultaneous Equation Chapter 5 Exercise 5.2 Solution|West Bengal Board Class 9 Math Book Solution.
Koshe Dekhi-5.2|কষে দেখি-৫.২
1. নীচের সমীকরণগুলির লেখচিত্র অঙ্কন করে সমাধানযোগ্য কিনা লিখি ও সমাধানযোগ্য হলে সমাধানটি বা অসংখ্য সমাধানের ক্ষেত্রে 3 টি সমাধান লিখি ।
(a) 2x +3y -7 = 0
3x+2y -8 = 0
(b) 4x-y = 11
-8x +2y = -22
(c ) 7x+3y = 42
21x +9y = 42
(d) 5x +y = 13
5x+ 5y = 12
সমাধানঃ
(a) 2x +3y -7 = 0
3x+2y -8 = 0
প্রদত্ত সহ সমীকরণদুটি হল –
2x +3y -7 = 0 —(i)
3x+2y -8 = 0 —(ii)
(i) নং সমীকরণ থেকে পাই ,
2x = 7 -3y
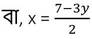
| x | 2 | 5 | -4 |
| y | 1 | -1 | 5 |
(ii) নং সমীকরণ থেকে পাই ,
3x+2y -8 = 0
বা,3x = 8-2y
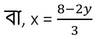
| x | 0 | 2 | -2 |
| y | 4 | 1 | 7 |
ছক কাগজে XOX´ এবং YOY´ দুটি পরস্পর লম্ব অঙ্কন করে , ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (2,1) ,(5,-1) এবং (-4,5) বিন্দুগুলি স্থাপন করে AB এবং (0,4) ,(4,-2) এবং (-2,7) বিন্দুগুলি স্থাপন করে CD সরলরেখা অঙ্কন করা হল
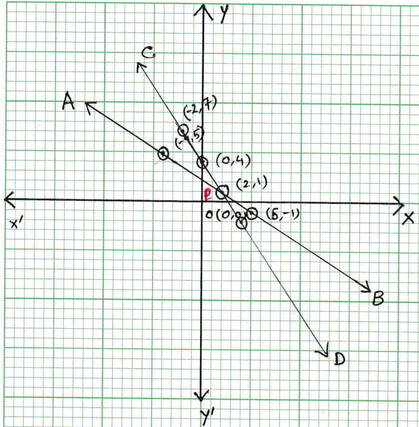
AB ও CD সরলরেখাদ্বয় পরস্পরকে P বিন্দুতে ছেদ করে । P বিন্দুর স্থানাঙ্ক (2,1)
∴ সমীকরণদুটির সাধারণ সমাধান , x =2 ,y = 1
(b) 4x-y = 11
-8x +2y = -22
প্রদত্ত সহসমীকরণ দুটি হল –
4x-y = 11 —(i)
-8x +2y = -22 —(ii)
(i) নং সমীকরণ থেকে পাই ,
4x-y = 11
বা, 4x = 11+y
বা, x = (11+y) /4
| x | 3 | 2 | 4 |
| y | 1 | -3 | 5 |
(ii) নং সমীকরণ থেকে পাই ,
-8x +2y = -22
বা, -8x = -22 -2y
বা, x = (-22-2y)/-8
| x | 3 | 2 | 4 |
| y | 1 | -3 | 5 |
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অঙ্কন করে ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (i) নং ও (ii) নং সমীকরণের লেখচিত্র অঙ্কন করা হল । দেখা যাচ্ছে লেখচিত্রদ্বয় পরস্পর সমপাতিত হয়ে AB সরলরেখা তৈরি হয়েছে সুতরাং প্রদত্ত সমীকরণদ্বয়ের অসংখ্য সমাধান থাকবে ।
∴ সমীকরণ দুটির তিনটি সাধারণ সমাধান ,
x =3 ,y = 1
x =2 ,y = -3
এবং x =4 , y = 5
(c ) 7x+3y = 42
21x +9y = 42
প্রদত্ত সহ সমীকরণদ্বয় হল –
7x+3y = 42 —(i)
-8x +2y = -22 —(ii)
(i) নং সমীকরণ থেকে পাই ,
7x = 42 -3y
বা, x = (42 -3y)/7
| x | 6 | 3 | 9 |
| y | 0 | 7 | -7 |
(ii) নং সমীকরণ থেকে পাই ,
21x +9y = 42
বা, 21x = 42y -9y
বা, x = (42-9y) /21
| x | 2 | -1 | 5 |
| y | 0 | 7 | -7 |
ছক কাগজে XOX´ এবং YOY´ দুটি পরস্পর লম্ব অঙ্কন করে , ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (6,0) ,(3,7) এবং (9,-7) বিন্দুগুলি স্থাপন করে AB এবং এবং (2,0) ,( -1,7) এবং (5,-7) বিন্দুগুলি স্থাপন করে CD সরলরেখা অঙ্কন করা হল ।

লেখচিত্র থেকে পরিস্কার যে, AB এবং CD সরলরেখাদ্বয় পরস্পর সমান্তরাল । তাই এক্ষেত্রে সমীকরণদ্বয়ের সমাধানযোগ্য নয় ।
(d) 5x +y = 13
5x+ 5y = 12
প্রদত্ত সহ সমীকরণদ্বয় হল –
5x +y = 13
বা, x = (13-y) /5
| x | 1 | 2 | 3 |
| y | 8 | 3 | -2 |
আবার , 5x+5y = 12
বা, 5x= 12-5y
বা, x = (12-5y) /5
| x | 12/5 | 2/5 | 0 |
| y | 0 | 2 | 12/5 |
ছক কাগজে XOX´ এবং YOY´ দুটি পরস্পর লম্ব অঙ্কন করে , ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (1,8) ,(2,3) এবং (3,-2) বিন্দুগুলি স্থাপন করে AB এবং এবং (12/5,0) ,(2/5 ,2) এবং (0, 12/5) বিন্দুগুলি স্থাপন করে CD সরলরেখা অঙ্কন করা হল ।
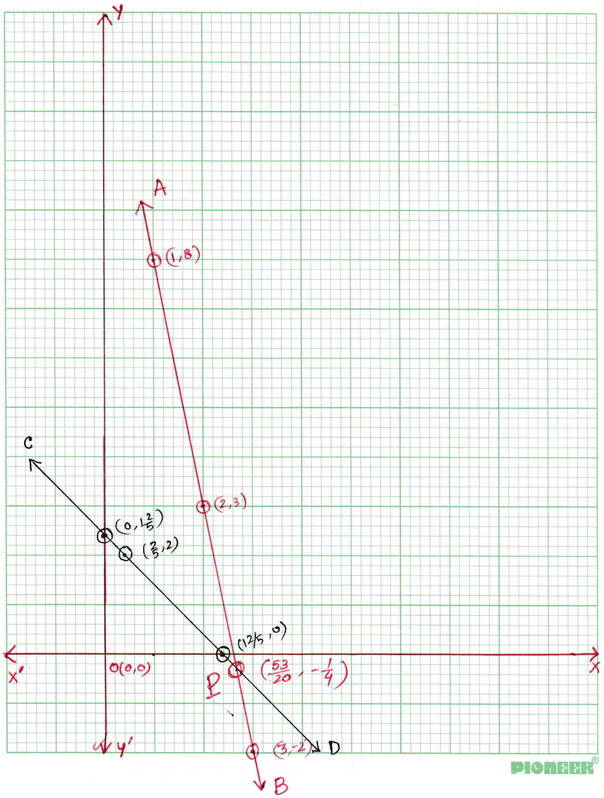
AB ও CD সরলরেখা পরস্পরকে P বিন্দুতে ছেদ করে । সুতরাং সমীকরণদ্বয় সমাধানযোগ্য । P বিন্দুর স্থানাঙ্ক (53/20 , -1/4)
∴ সমীকরণদুটির সাধারণ সমাধান x = 53/20 এবং y = -1/4
2. নীচের প্রতিজোড়া সমীকরণগুলির একই চলের সহগগুলির একই চলের সহগ গুলির ও ধ্রুবক গুলির অনুপাতের সম্পর্ক নির্ণয় করে সমীকরণ দুটি সমাধানযোগ্য কিনা লিখি ও সমীকরণগুলির লেখচিত্র এঁকে যাচাই করি ।
(a) x+5y = 7 , x+5y = 20
সমাধানঃ প্রদত্ত সহ সমীকরণদ্বয় হল –
x+5y = 7 —(i)
বা, x+5y-7 = 0
এবং , x+5y = 20 —(ii)
বা, x+5y -20 = 0
সমীকরণদ্বয়ের, x- এর সহগদ্বয়ের অনুপাত = 1:1, y –এর সহগ দ্বয়ের অনুপাত = 5:5 = 1:1 এবং ধ্রুবক পদের অনুপাত = 7 :20
∴ x- এর সহগদ্বয়ের অনুপাত = y –এর সহগ দ্বয়ের অনুপাত ≠ ধ্রুবক পদের অনুপাত
সুতরাং সমীকরণদ্বয় সমাধানযোগ্য নয় ।
লেখচিত্রের মাধ্যমে যাচাইঃ
(i) নং সমীকরণ থেকে পাই ,
x+5y-7 = 0
বা, x = 7-5y
| x | 7 | 2 | -3 |
| y | 0 | 1 | 2 |
(ii) নং সমীকরণ থেকে পাই ,
x+5y = 20
বা, x = 20-5y
| x | 0 | 10 | 5 |
| y | 4 | 2 | 3 |
ছক কাগজে XOX´ এবং YOY´ দুটি পরস্পর লম্ব অঙ্কন করে , ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (7,0) ,(-3,2) এবং (2,1) বিন্দুগুলি স্থাপন করে AB এবং (0,4) ,(10,2) এবং (5,3) বিন্দুগুলি স্থাপন করে CD সরলরেখা অঙ্কন করা হল ।

লেখচিত্র থেকে পরিস্কার যে , AB এবং CD সরল রেখাদ্বয় পরস্পর সমান্তরাল । তাই সেক্ষেত্রে সমীকরণদ্বয় সমাধানযোগ্য নয় ।
(b) 2x+y = 8 , 2y -3x= -5
সমাধানঃ প্রদত্ত সহ সমীকরণদ্বয় হল-
2x+y = 8 —(i)
বা, 2x+y -8 = 0
এবং , 2y -3x= -5 —(ii)
বা, -3x +2y +5 = 0
এখন , x- এর সহগদ্বয়ের অনুপাত = 2 : -3 , y –এর সহগ দ্বয়ের অনুপাত = 1:2 এবং ধ্রুবক পদের অনুপাত = -8 : 5
∴ x- এর সহগদ্বয়ের অনুপাত ≠ y –এর সহগ দ্বয়ের অনুপাত ≠ ধ্রুবক পদের অনুপাত
সুতরাং, সমীকরণদ্বয় সমাধানযোগ্য এবং সমীকরণদ্বয়ের একটি সাধারণ সমাধান থাকবে ।
লেখচিত্রের সাহায্যে যাচাই:
(i) নং সমীকরণ থেকে পাই ,
2x = 8-y
বা, x = (8-y) /2
| x | 4 | 0 | 8 |
| y | 0 | 8 | -8 |
(ii) নং সমীকরণ থেকে পাই ,
2y -3x= -5
বা, -3x = -2y -5
বা, 3x = 2y+5
বা, x = (2y +5) /3
| x | 3 | 5 | -1 |
| y | 2 | 5 | -4 |
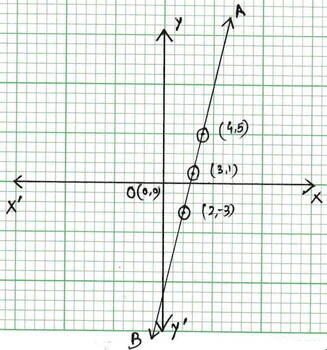
ছক কাগজে XOX´ এবং YOY´ দুটি পরস্পর লম্ব অঙ্কন করে , ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (4,0) ,(0,8) এবং (8,-8) বিন্দুগুলি স্থাপন করে AB এবং (3,2) ,(5,5) এবং (-1,-4) বিন্দুগুলি স্থাপন করে CD সরলরেখা অঙ্কন করা হল ।
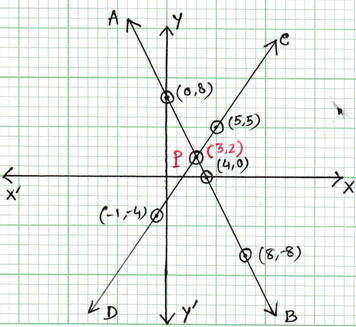
AB ও CD সরলরেখা পরস্পরকে P বিন্দুতে ছেদ করেছে । P বিন্দুর স্থানাঙ্ক (3,2)
∴ সমীকরণদুটির সাধারণ সমাধান হল x = 3 এবং y = 2 ।
(c ) 5x+8y = 14 , 15x+24y = 42
সমাধানঃ প্রদত্ত সহ সমীকরণদ্বয় হল –
5x+8y = 14 —(i)
বা, 5x +8y -14 = 0
এবং, 15x+24y = 42 —(ii)
বা, 15x + 24y -42 = 0
এখন , xএর সহগদ্বয়ের অনুপাত = 5 : 15 = 1:3 , y এর সহগদ্বয়ের অনুপাত = 8 : 24 = 1:3 এবং ধ্রুবক পদের অনুপাত = – 14: -42 = 1:3
∴ xএর সহগদ্বয়ের অনুপাত = y এর সহগদ্বয়ের অনুপাত = ধ্রুবক পদের অনুপাত
∴ সুতরাং , সমীকরণদ্বয় সমাধানযোগ্য কিন্তু এদের অসংখ্য সাধারণ সমাধান থাকবে ।
লেখচিত্রের মাধ্যমে যাচাইঃ
(i) নং সমীকরণ থেকে পাই ,
5x + 8y = 14
বা, 5x = 14-8y
বা, x = (14-8y) /5
| x | 6 | -2 | -10 |
| y | -2 | 3 | 8 |
আবার , (ii) নং সমিকরণ থেকে পাই ,
15x+24y =42
বা, (5x+8y ) = 14
বা, x = (14-8y) / 5
| x | 6 | -2 | -10 |
| y | -2 | 3 | 8 |
ছক কাগজে XOX´ এবং YOY´ দুটি পরস্পর লম্ব অঙ্কন করে , ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (i) ও (ii) নং সমীকরণের লেখচিত্রদ্বয় অঙ্কন করা হয়েছে এবং তারা পরস্পর সমপাতিত হয়ে একটি সরলরেখা AB তৈরি হয়েছে ।
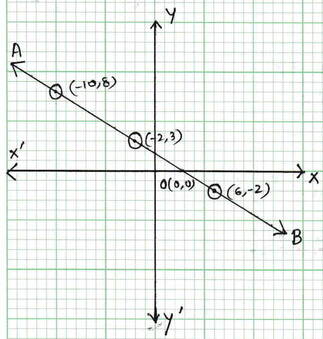
যেহেতু, সরলরেখাদ্বয় পরস্পর সমপাতিত হয়েছে , সুতরাং সমীকরণদ্বয়ের অসংখ্য সাধারণ সমাধান থাকবে ।
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
| WBBSE Class 9 Math Koshe Dekhi 5.2.রৈখিক সহসমীকরণ (দুই চল বিশিষ্ট )কষে দেখি ৫.২|Ganit Prakash Class 9 Koshe Dekhi 5.2 Solution|Ganit Prakash Class Nine Koshe Dekhi 5.2 Somadhan|গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.২ সমাধান|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.২ সমাধান|Linear Simultaneous Equation Chapter 5 Exercise 5.2 Solution|West Bengal Board Class 9 Math Book Solution. |
(d) 3x+2y = 6 , 12x+8y = 24
সমাধানঃ প্রদত্ত সহ সমীকরণদ্বয় হল
3x+2y = 6 —(i)
বা, 3x +2y -6 = 0
এবং, 12x+8y = 24 —(ii)
বা, 12x +8y -24 = 0
এখন সমীকরণদ্বয়ের, x এর সহগদ্বয়ের অনুপাত = 3 :12 = 1:4,y এর সহগদ্বয়ের অনুপাত = 2 :8 = 1:4 এবং ধ্রুবক পদের অনুপাত = -6 : -24 = 1:4
∴ x এর সহগদ্বয়ের অনুপাত = y এর সহগদ্বয়ের অনুপাত = ধ্রুবক পদের অনুপাত
∴ প্রদত্ত সমীকরণদ্বয়ের অসংখ্য সমাধান থাকবে ।
লেখচিত্রের মাধ্যমে যাচাইঃ
(i) নং সমীকরণ থেকে পাই ,
3x+2y = 6
বা, 3x = 6 -2y
বা, x = (6-2y) /3
| x | -2 | 0 | 4 |
| y | 6 | 3 | -3 |
(ii) নং সমীকরণ থেকে পাই ,
12x+8y = 24
বা, x = (24 -8y) / 12
বা, x = (6-2y) /3
| x | -2 | 0 | 4 |
| y | 6 | 3 | -3 |
ছক কাগজে XOX´ এবং YOY´ দুটি পরস্পর লম্ব অঙ্কন করে , ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (i) ও (ii) নং সমীকরণের লেখচিত্রদ্বয় অঙ্কন করা হয়েছে এবং তারা পরস্পর সমপাতিত হয়ে একটি সরলরেখা AB তৈরি হয়েছে ।
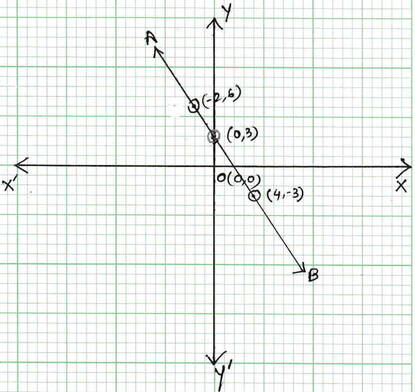
যেহেতু, সরলরেখাদ্বয় পরস্পর সমপাতিত হয়েছে , সুতরাং সমীকরণদ্বয়ের অসংখ্য সাধারণ সমাধান থাকবে ।
3. নীচের প্রতিজোড়া সমীকরণগুলি একই চলের সহগগুলির ও ধ্রুবকগুলির অনুপাতের সম্পর্ক নির্ণয় করে সমীকরণ গুলির লেখচিত্র গুলি সমান্তরাল বা পরস্পর ছেদি বা সমপাতিত হবে কিনা লিখি ।
(a) 5x+3y = 11, 2x -7y = -12
সমাধানঃ প্রদত্ত সহসমীকরণদ্বয় হল –
5x+3y = 11
বা, 5x +3y – 11 = 0
এবং 2x -7y = -12
বা, 2x – 7y +12 = 0
∴ সমীকরণদ্বয়ের , x এর সহগদ্বয়ের অনুপাত = 5 :2 ,y এর সহগদ্বয়ের অনুপাত = 3 : -7 এবং ধ্রুবকপদের অনুপাত = – 11 : 12
∴ x এর সহগদ্বয়ের অনুপাত ≠ y এর সহগদ্বয়ের অনুপাত ≠ ধ্রুবকপদের অনুপাত
∴ প্রদত্ত সমীকরণদ্বয়ের লেখচিত্র দুটি পরস্পরছেদী হবে ।
(b) 6x -8y = 2 , 3x-4y = 1
সমাধানঃ প্রদত্ত সমীকরণদ্বয় হল –
6x -8y = 2
বা, 6x – 8y -2 = 0
এবং, 3x-4y = 1
বা, 3x -4y -1 = 0
∴ সমীকরণদ্বয়ের , x এর সহগদ্বয়ের অনুপাত = 6 :3 = 2:1 , y এর সহগদ্বয়ের অনুপাত = -8 : -4 = 2:1 এবং ধ্রুবক পদের অনুপাত = -2 : -1 = 2:1
∴ x এর সহগদ্বয়ের অনুপাত = y এর সহগদ্বয়ের অনুপাত = ধ্রুবক পদের অনুপাত
∴ প্রদত্ত সমীকরণদ্বয়ের লেখচিত্রগুলি সমপাতিত হবে ।
(c ) 8x-7y= 0 , 8x-7y = 56
সমাধানঃ প্রদত্ত সমীকরণদ্বয় হল –
8x-7y= 0
এবং , 8x-7y = 56
বা, 8x -7y -56 = 0
∴ সমীকরণদ্বয়ের , x এর সহগদ্বয়ের অনুপাত = 8:8 = 1:1 , y এর সহগদ্বয়ের অনুপাত = -7 : -7 = 1:1 এবং ধ্রুবক পদের অনুপাত = 0 : -56
∴ x এর সহগদ্বয়ের অনুপাত = y এর সহগদ্বয়ের অনুপাত ≠ ধ্রুবক পদের অনুপাত
∴ প্রদত্ত সমীকরণদ্বয়ের লেখচিত্রগুলি সমান্তরাল হবে ।
(d ) 4x-3y = 6 , 4y-5x = -7
সমাধানঃ প্রদত্ত সমীকরণদ্বয় হল –
4x-3y = 6
বা, 4x -3y -6 =0
এবং, 4y-5x = -7
বা, -5x +4y +7 = 0
∴ x –এর সহগদ্বয়ের অনুপাত = 4 : -5 , y এর সহগ দ্বয়ের অনুপাত = -3 : 4 এবং ধ্রুবকপদের অনুপাত = -6 : 7
∴ x এর সহগদ্বয়ের অনুপাত ≠ y এর সহগদ্বয়ের অনুপাত ≠ ধ্রুবকপদের অনুপাত
∴ প্রদত্ত সমীকরণদ্বয়ের লেখচিত্রদ্বয় পরস্পরছেদী হবে ।
4. নীচের প্রতিজোড়া সমীকরণ গুলির মধ্যে যেগুলি সমাধানযোগ্য তাদের লেখচিত্র এঁকে সমাধান করি এবং অসংখ্য সমাধানের ক্ষেত্রে 3 টি সমাধান লিখি ।
(a) 4x+3y =20 , 8x+6y = 40
সমাধানঃ প্রদত্ত সমীকরণদ্বয় হল –
4x+3y = 20
বা,4x +3y -20 = 0
এবং , 8x+6y = 40
বা, 8x +6y – 40 = 0
বা, 4x +3y -20 = 0
সমীকরণ দ্বয়ের x এর সহগদ্বয়ের অনুপাত = 4 :4 = 1:1 , y –এর সহগদ্বয়ের অনুপাত = 6:6 = 1:1 এবং ধ্রুবক পদের অনুপাত = – 20 : -20 = 1: 1
∴ x এর সহগদ্বয়ের অনুপাত = y এর সহগদ্বয়ের অনুপাত = ধ্রুবক পদের অনুপাত
সুতরাং ,সহসমীকরণদ্বয়ের লেখচিত্রদুটি পরস্পর সমপাতিত হবে এবং সমীকরণ দ্বয়ের অসংখ্য সমাধান থাকবে ।
(i) নং সমীকরণ থেকে পাই ,
4x+3y = 20
বা, 4x = 20 – 3y
বা, x = (20-3y) / 4
| x | 5 | 2 | -1 |
| y | 0 | 4 | 8 |
(ii) নং সমীকরণ থেকে পাই ,
4x+3y = 20
বা, 4x = 20 – 3y
বা, x = (20-3y)/4
| x | 5 | 2 | -1 |
| y | 0 | 4 | 8 |
দুটি সমীকরণ একই তাই সমীকরণ দুটির অসংখ্য সমাধান থাকবে ।
∴ সমীকরণদুটির 3 টি সাধারণ সমাধান হল (x=5, y=0) ,(x=2,y=4) এবং (x=-1 ,y=8)
(b) 4x+3y = 20 , 12x +9y = 20
সমাধানঃ প্রদত্ত সমীকরণদ্বয় হল –
4x+3y = 20
বা, 4x +3y – 20 = 0
এবং, 12x +9y = 20
বা, 12x+9y -20 = 0
সমীকরণদ্বয়ের , x এর সহগদ্বয়ের অনুপাত 4 :12 = 1:3 , y –এর সহগদ্বয়ের অনুপাত = 3:9 = 1:3 এবং ধ্রুবক পদের অনুপাত = 20 :20 = 1:1
∴ x এর সহগদ্বয়ের অনুপাত = y –এর সহগদ্বয়ের অনুপাত ≠ ধ্রুবক পদের অনুপাত
∴ প্রদত্ত সমীকরণদ্বয়ের কোনো সমাধান থাকবে না ।
(c ) 4x+3y = 20 , 3x/4 – y/8 = 1
সমাধানঃ প্রদত্ত সমীকরণদ্বয় হল –
4x+3y = 20 —-(i)
বা, 4x+3y -20 = 0
এবং , 3x/4 – y/8 = 1—(ii)
বা, (6x-y) /8 = 1
বা, 6x-y = 8
বা, 6x-y -8 = 0
সমীকরণদ্বয়ের , x এর সহগদ্বয়ের অনুপাত = 4 :6 = 2:3 ,y এর সহগ দ্বয়ের অনুপাত = 3 : -1 এবং ধ্রুবক পদের অনুপাত = – 20 : -8 = 5 : 2
∴ x এর সহগদ্বয়ের অনুপাত ≠ y এর সহগ দ্বয়ের অনুপাত
∴ সমীকরণ দ্বয়ের একটি নির্দিষ্ট সাধারণ সমাধান থাকবে ।
(i) নং সমীকরণ থেকে পাই ,
4x+3y = 20
বা, 4x = 20 -3y
বা, x = (20 -3y) /4
| x | 5 | 2 | -1 |
| y | 0 | 4 | 8 |
(ii) নং সমীকরণ থেকে পাই ,
6x –y = 8
বা, 6x = 8+y
বা, x = (8+y) /6
| x | 1 | 2 | 0 |
| y | -2 | 4 | -8 |
ছক কাগজে XOX´ এবং YOY´ দুটি পরস্পর লম্ব অঙ্কন করে , ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (5,0) ,(2,4) এবং (-1,8) বিন্দুগুলি স্থাপন করে AB এবং এবং (1,-2) ,( 2,4) এবং (0,-8) বিন্দুগুলি স্থাপন করে CD সরলরেখা অঙ্কন করা হল ।
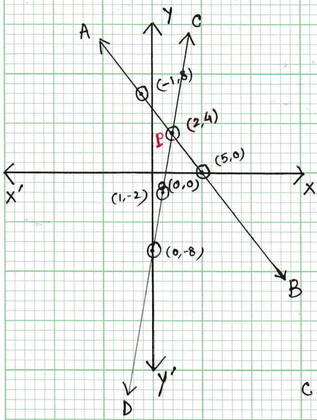
AB ও CD সরলরেখা পরস্পরকে P বিন্দুতে ছেদ করে । P বিন্দুর স্থানাঙ্ক (2,4)
∴ সমীকরণদুটির সাধারণ সমাধান হল x =2 এবং y = 4
(d) p-q = 3 , p /3 +q/2 = 6
সমাধানঃ প্রদত্ত সমীকরণদ্বয় হল-
p-q = 3 —(i)
বা, p-q-3 = 0
এবং , p /3 +q/2 = 6 —(ii)
বা, (2p+3q ) / 10 = 36
বা, 2p + 3q = 36
বা, 2p +3q – 36 = 0
সমীকরণদ্বয়ের , p এর সহগদ্বয়ের অনুপাত = 1 :2 ,q –এর সহগদ্বয়ের অনুপাত = -1 :5 এবং ধ্রুবক পদের অনুপাত = -3 : -60 = 1:20
∴ p এর সহগদ্বয়ের অনুপাত ≠ q –এর সহগদ্বয়ের অনুপাত
∴ সমীকরণ দ্বয়ের একটি নির্দিষ্ট সাধারণ সমাধান বর্তমান ।
(i) নং সমীকরণ থেকে পাই ,
p-q =3
বা, p = 3+q
| p | 3 | 7 | 0 |
| q | 0 | 4 | -3 |
(ii) নং সমীকরণ থেকে পাই ,
p/3 +q/2 = 6
বা, 2p +3q = 36
বা, p = (36 -3q) /2
| p | 6 | 0 | 3 |
| q | 8 | 12 | 10 |
ছক কাগজে XOX´ এবং YOY´ দুটি পরস্পর লম্ব অঙ্কন করে , ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (3,0) ,(7,4) এবং (0,-3) বিন্দুগুলি স্থাপন করে AB এবং এবং (6,8) ,(0,12) এবং (3,10) বিন্দুগুলি স্থাপন করে CD সরলরেখা অঙ্কন করা হল ।

AB ও CD সরলরেখা পরস্পরকে P বিন্দুতে ছেদ করে । P বিন্দুর স্থানাঙ্ক (9 ,6)
∴ সমীকরণ দুটির সাধারণ সমাধান হল p = 9 ,q = 6
(e ) p-q =3 , p /5 –q/5 =3
সমাধানঃ p-q = 3
বা, p –q -3 = 0
এবং , p/5 –q/5 = 3
বা, p-q = 15
বা, p-q -15 = 0
সমীকরণদ্বয়ের , p এর সহগদ্বয়ের অনুপাত = 1 :1 , q এর সহগদ্বয়ের অনুপাত = -1 : -1 = 1 :1 এবং ধ্রুবক পদের অনুপাত = -3 : -15 = 1:5
∴ p এর সহগদ্বয়ের অনুপাত = q এর সহগদ্বয়ের অনুপাত ≠ ধ্রুবক পদের অনুপাত
∴ সমীকরণদ্বয়ের সমাধান সম্ভব নয় ।
(f ) p –q = 3 , 8p-8q -3 = 0
সমাধানঃ প্রদত্ত সমীকরণদ্বয় হল –
p –q = 3
বা, p –q -3 = 0
8p-8q -3 = 0
সমীকরণদ্বয়ের, p এর সহগদ্বয়ের অনুপাত = 1:8 , q এর সহগদ্বয়ের অনুপাত = -1 :-8 = 1:8 এবং ধ্রুবক পদের অনুপাত = -3 : -3 = 1:1
∴ p এর সহগদ্বয়ের অনুপাত = q এর সহগদ্বয়ের অনুপাত ≠ ধ্রুবক পদের অনুপাত
সুতরাং , সমীকরণ দ্বয়ের সমাধান সম্ভব নয় ।
5. তথাগত একটি দুইচল বিশিষ্ট একঘাত সমীকরণ x+y = 5 লিখেছে । আমি আর একটি দুইচল বিশিষ্ট একঘাত সমীকরণ লিখি যাতে দুটি সমীকরণের লেখচিত্র
(a)পরস্পর সমান্তরাল হবে
উত্তরঃ x+y = 7
(b)পরস্পর ছেদি হবে
উত্তরঃ 2x+3y = 20
(c )পরস্পর সমপাতিত হবে
উত্তরঃ 2x+2y = 10
| WBBSE Class 9 Math Koshe Dekhi 5.2.রৈখিক সহসমীকরণ (দুই চল বিশিষ্ট )কষে দেখি ৫.২|Ganit Prakash Class 9 Koshe Dekhi 5.2 Solution|Ganit Prakash Class Nine Koshe Dekhi 5.2 Somadhan|গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.২ সমাধান|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.২ সমাধান|Linear Simultaneous Equation Chapter 5 Exercise 5.2 Solution|West Bengal Board Class 9 Math Book Solution. |
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন