Ganit Prabha Class 7 Koshe Dekhi 12.2|বীজগাণিতিক সূত্রাবলী কষে দেখি ১২.২|গণিতপ্রভা ক্লাস ৭ অধ্যায় ১২ কষে দেখি ১২.২ সমাধান|WBBSE Class 7(Seven/VII) Chapter 12 Exercise 12.2 Solution
Ganit Prabha Class 7 Koshe Dekhi 12.2|বীজগাণিতিক সূত্রাবলী কষে দেখি ১২.২|গণিতপ্রভা ক্লাস ৭ অধ্যায় ১২ কষে দেখি ১২.২ সমাধান|WBBSE Class 7(Seven/VII) Chapter 12 Exercise 12.2 Solution
কষে দেখি – 12.2
1. (x + a) (x + b) = x2 + (a + b) x + ab -এই অভেদের সাহায্যে নীচের বীজগাণিতিক সংখ্যামালাগুলি গুণ করি ।
(i) (x + 7) (x + 1)
সমাধানঃ
(x + 7) (x + 1)
= x2 + (7 + 1) x + 7 + 1
= x2 + 8x + 7
(ii) (x – 8) (x – 2)
সমাধানঃ
(x – 8) (x – 2)
= {x +(-8)}{x+(-2)}
= x2 + {(-8) + (-2)}x + 8×2
= x2 + (-8-2)x + 16
= x2 + (-10)x + 16
= x2 – 10x +16
(iii) (x + 9) (x – 6)
সমাধানঃ
(x + 9) (x – 6)
= (x + 9) {x + (- 6)}
= x2 + {9 + (-6)} x + 9 × (-6)
= x2 + 3x – 54
(iv) (2x + 1) (2x – 1)
সমাধানঃ
(2x + 1) (2x – 1)
= (2x)2 + {1 + (-1)}2x + 1 × (-1)
=4x2 + 0 × 2x – 1
= 4x2 – 1
(v) (xy – 4) (xy + 2)
সমাধানঃ
(xy – 4) (xy + 2)
= (xy)2 + {-4 + 2} xy + (-4) × 2
= x2y2 + (-2) × xy – 8
= x2y2 – 2xy – 8
(vi) (a2 + 5) (a2 – 4)
সমাধানঃ
(a2 + 5) (a2 – 4)
= (a2)2 + (5 – 4)a2 + 5 × (-4)
=a4 + a2 – 20
2. সূত্রের সাহায্যে দেখাই যে –
(i) (2x + 3y)2 – (2x – 3y)2 = 24xy
সমাধানঃ
বামপক্ষ = (2x + 3y)2 – (2x – 3y)2
= 4 × 2x × 3y
= 24xy
= ডানপক্ষ
∴ বামপক্ষ = ডানপক্ষ [প্রমানিত]
(ii) (a + 2b)2 + (a – 2b)2 = 2(a2 + 4b2)
সমাধানঃ
বামপক্ষ = (a + 2b)2 + (a – 2b)2
= 2{(a)2 +(2b)2}
= 2(a2 + 4b2)
= ডানপক্ষ
∴ বামপক্ষ = ডানপক্ষ [প্রমানিত]
(iii) (l + m)2 = (l – m)2 + 4lm
সমাধানঃ
বামপক্ষ = (l + m)2
= l2 + m2 + 2lm
= l2 + m2 – 2lm +4lm
= (l – m)2 + 4lm
= ডানপক্ষ
∴ বামপক্ষ = ডানপক্ষ [প্রমানিত]
(iv) (2p – q)2 = (2p +q)2 – 8pq
সমাধানঃ
বামপক্ষ = (2p – q)2
= (2p + q)2 – 4.2p.q
= (2p + q)2 – 8pq
= ডানপক্ষ
∴ বামপক্ষ = ডানপক্ষ [প্রমানিত]
(v) (3m + 4n)2 = (3m – 4n)2 + 48mn
সমাধানঃ
বামপক্ষ =(3m + 4n)2
= (3m – 4n)2 + 4.3m. 4n
= (3m – 4n)2 + 48mn
= ডানপক্ষ
∴ বামপক্ষ = ডানপক্ষ [প্রমানিত]
(vi) (6x + 7y)2 – 84xy = 36x2 + 49y2
সমাধানঃ
বামপক্ষ = (6x + 7y)2 – 84xy
= (6x + 7y)2 – 2.6x. 7y
= (6x)2 + (7y)2
= 36x2 + 49y2
= ডানপক্ষ
∴ বামপক্ষ = ডানপক্ষ [প্রমানিত]
(vii) (3a – 4b)2 + 24ab = 9a2 + 16b2
সমাধানঃ
বামপক্ষ = (3a – 4b)2 + 24ab
= (3a – 4b)2 – 2.3a. 4b
= (3a)2 + (4b)2
= 9a2 + 16b2
= ডানপক্ষ
∴ বামপক্ষ = ডানপক্ষ [প্রমানিত]

∴ বামপক্ষ = ডানপক্ষ [প্রমানিত]
3. প্রতিক্ষেত্রে সূত্রের সাহায্যে সমস্যার সমাধান করি ।
(i) x – y = 3, xy = 28 হলে x2 + y2 -এর মান কত লিখি ।
সমাধানঃ
x2 + y2 = (x – y)2 +2xy
= (3)2 + 2 × 28
= 9 + 56
= 65
(ii) a2 + b2 = 52, a – b = 2 হলে, ab -এর মান কত লিখি ।
সমাধানঃ
a2 + b2= (a – b)2 + 2ab
বা, 52 = (2)2 + 2ab
বা, 4 + 2ab = 52
বা, 2b = 52 – 4
বা, ab = 48 /2
∴ ab = 24
Ganit Prabha Class 7 Koshe Dekhi 12.2|বীজগাণিতিক সূত্রাবলী কষে দেখি ১২.২|গণিতপ্রভা ক্লাস ৭ অধ্যায় ১২ কষে দেখি ১২.২ সমাধান|WBBSE Class 7(Seven/VII) Chapter 12 Exercise 12.2 Solution
(iii) l2 + m2 = 13 এবং l + m = 5 হলে lm -এর মান কত লিখি ।
সমাধানঃ
l2 + m2 = 13 = (l + m)2 – 2lm
বা, 13 = (5)2 – 2lm
বা, 2lm = 25 – 13
বা, 2lm = 12
বা, lm = 12/2
∴ lm = 6
(iv) a+ 1/a = 4 হলে a2+1/a2 -এর মান কত লিখি ।
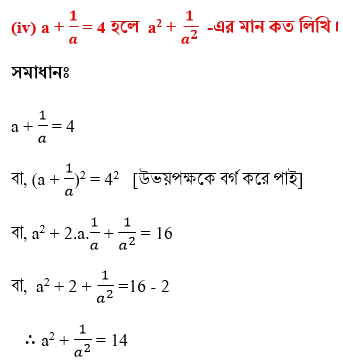
| Ganit Prabha Class 7 Koshe Dekhi 12.2|বীজগাণিতিক সূত্রাবলী কষে দেখি ১২.২|গণিতপ্রভা ক্লাস ৭ অধ্যায় ১২ কষে দেখি ১২.২ সমাধান|WBBSE Class 7(Seven/VII) Chapter 12 Exercise 12.2 Solution |
(v) a-1/a = 4 হলে , a2 +1/a2 -এর মান লিখি ।
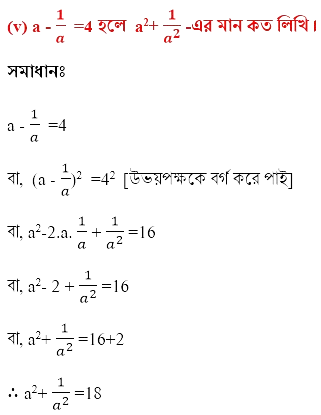
(vi) 5x+1/x = 6 হলে , দেখাই যে 25x2 +1/x2 =26

(vii) 2x+ 1/x =5 হলে , 4x2 +1/x2 -এর মান লিখি ।

(viii) x/y +y/x =3 হলে , x2/y2 +y2/x2 -এর মান লিখি ।

(ix) x2 + y2 = 4xy হলে প্রমাণ করি যে x4 + y4 = 14x2y2
সমাধানঃ
x2 + y2 = 4xy
বা, (x2 + y2)2 = (4xy)2 [উভয়পক্ষকে বর্গ করে পাই]
বা, (x2)2 + 2x2y2 + (y2)2 = (4xy)2
বা, x4 + 2x2y2 + y4 = 16x2y2
বা, x4 + y4 = 16x2y2 – 2x2y2
∴ x4 + y4 = 14x2y2 [প্রমানিত]
(x) 2a +1/3a = 6 হলে , 4a2 +1/9a2 -এর মান কত লিখি ।

(xi) 5a +1/7a = 5 হলে , 25a2 +1/49a2 -এর মান কত লিখি ।

(xii) 2x -1/x =4 হলে , x2 +1/4x2 -এর মান লিখি ।

(xiii) m+1/m= -p হলে দেখাই যে , m2 +1/m2 = p2-2
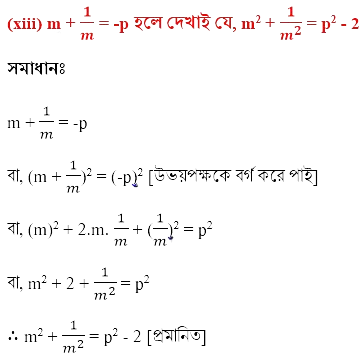
(xiv) a2+b2=5ab হলে দেখাই যে a2/b2 +b2/a2=23

| Ganit Prabha Class 7 Koshe Dekhi 12.2|বীজগাণিতিক সূত্রাবলী কষে দেখি ১২.২|গণিতপ্রভা ক্লাস ৭ অধ্যায় ১২ কষে দেখি ১২.২ সমাধান|WBBSE Class 7(Seven/VII) Chapter 12 Exercise 12.2 Solution |
(xv) 6x2-1 =4x হলে , দেখাই যে 36x2 +1/x2 =28

(xvi) m-1/m =p-2 হলে , দেখাই যে m2+1/m2=p2-4p+6

(xvi) m- 1/m =p-2 হলে দেখাই যে , m2 +1/m2=p2-4p+6

ধন্যবাদ ।এই POST টি আপনাদের ভালো লাগলে SHARE করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পাওয়ার জন্য আমাদের FACEBOOK PAGE টি LIKE করুন ।
This is very helpful post for class 7 wbbse students.