![Koshe Dekhi 5.3 Class 10 [PDF]
অনুপাত সমানুপাত কষে দেখি ৫.৩](https://anushilan.com/wp-content/uploads/2022/03/কষে-দেখি-5.3-ক্লাস-10-অনুপাত-সমানুপাত-.jpeg)
Koshe Dekhi 5.3 Class 10 | অনুপাত সমানুপাত কষে দেখি ৫.৩ দশম শ্রেণী (ক্লাস ১০) | গণিত প্রকাশ দশম শ্রেণি অনুপাত সমানুপাত কষে দেখি 5.3 সমাধান | WBBSE Madhyamik Class 10(Ten)(X) Chapter 5 (Ratio & Proportion) Exercise 5.3 Solution
Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩
1. a:b = c:d হলে দেখাই যে ,
(i) (a2+b2) : (a2-b2) = (ac+bd) : (ac-bd)
সমাধানঃ
ধরি , a:b = c:d = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ a= bk এবং c=dk
বামপক্ষ:
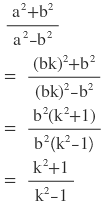
ডানপক্ষ:
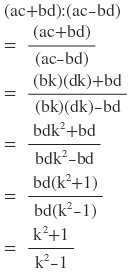
∴ বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]
1(ii) a:b = c:d হলে দেখাই যে ,
(a2+ab+b2) : (a2-ab+b2) = (c2+cd+d2) (c2-cd+d2)
সমাধান ঃ
ধরি , a:b = c:d = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ a= bk এবং c=dk
বামপক্ষঃ
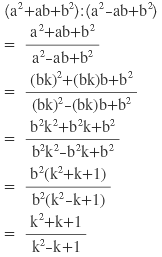
ডানপক্ষঃ
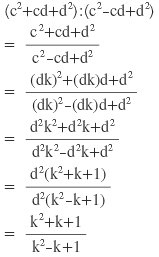
∴ বামপক্ষ = ডানপক্ষ [প্রমাণিত ]
Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩
1(iii) a:b = c:d হলে দেখাই যে ,
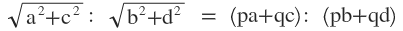
সমাধানঃ
ধরি , a:b = c:d = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ a= bk এবং c=dk
বামপক্ষঃ
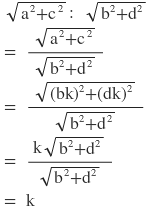
ডানপক্ষঃ
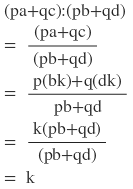
∴ বামপক্ষ =ডানপক্ষ [ প্রমাণিত ]
Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩
2(i) x:a = y:b = z:c হলে প্রমান করি যে ,
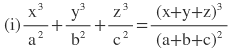
সমাধানঃ
ধরি , x:a = y:b = z:c = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ x= ak , y=bk, z = ck
বামপক্ষঃ
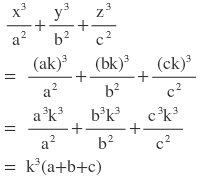
ডানপক্ষঃ
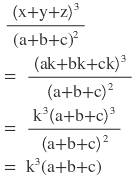
∴ বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
2(ii) x:a = y:b = z:c হলে প্রমান করি যে ,
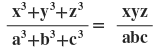
সমাধানঃ
ধরি , x:a = y:b = z:c = k [ k(≠0) একটি আনুপাতিক ধ্রুবক ]
∴ x= ak , y=bk, z = ck
বামপক্ষঃ
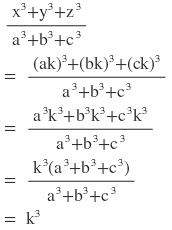
ডানপক্ষঃ
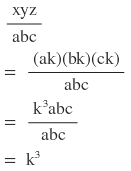
∴বামপক্ষ =ডানপক্ষ [ প্রমাণিত ]
Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩
2(iii) x:a = y:b = z:c হলে প্রমান করি যে ,
(a2+b2+c2)(x2+y2+z2) = (ax+by+cz)2
সমাধানঃ
ধরি , x:a = y:b = z:c = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ x= ak , y=bk, z = ck
বামপক্ষঃ
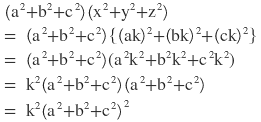
ডানপক্ষঃ
(ax+by+cz)2
= {a(ak)+b(bk)+c(ck)}2
= (a2k+b2k+c2k)2
= k2(a2+b2+c2)2
∴ বামপক্ষ = ডানপক্ষ [ প্রমানিত ]
3(i) . a:b = c:d = e:f হলে প্রমান করি যে,
প্রত্যেকটি অনুপাত = (5a-7c-13e) / (5b-7d-13f)
সমাধানঃ
ধরি , a:b = c:d = e:f = k
∴ a=bk , c=dk, e = fk [ k(≠0) একটি আনুপাতিক ধ্রুবক ]
∴ (5a-7c-13e) / (5b-7d-13f)
= {5(bk)-7(dk)-13(fk)} / (5b-7d-13f)
= k (5b-7d-13f)/ (5b-7d-13f)
= k
∴ প্রত্যেকটি অনুপাত = (5a-7c-13e) / (5b-7d-13f) [ প্রমাণিত ]
Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩
3(ii) a:b = c:d = e:f হলে প্রমান করি যে,
(a2+c2+e2)(b2+d2+f2) = (ab+cd+ef)2
সমাধানঃ
ধরি , a:b = c:d = e:f = k
∴ a=bk , c=dk, e = fk [ k(≠0) একটি আনুপাতিক ধ্রুবক ]
বামপক্ষঃ
(a2+c2+e2)(b2+d2+f2)
= {(bk)2+(dk)2+(fk)2} (b2+d2+f2)
= (b2k2+d2k2+f2k2)(b2+d2+f2)
= k2(b2+d2+f2)(b2+d2+f2)
= k2 (b2+d2+f2)2
ডানপক্ষঃ
(ab+cd+ef)2
= {(bk)b+(dk)d+(fk)f }2
= (b2k+d2k+f2k)2
= k2 (b2+d2+f 2)2
∴ বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]
4(i) যদি a:b = b:c হয় , তবে প্রমান করি যে ,
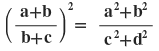
সমাধানঃ
ধরি a:b = b:c = k [ k(≠0) একটি আনুপাতিক ধ্রুবক ]
∴ a = bk এবং b = ck
আবার , a = (ck).k = ck2 , b = ck
বামপক্ষঃ
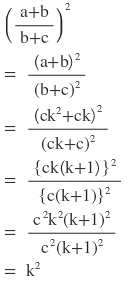
ডানপক্ষঃ
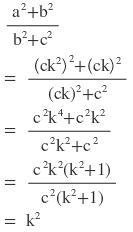
∴ বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]
| Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩ |
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
4(ii) যদি a:b = b:c হয় , তবে প্রমান করি যে ,
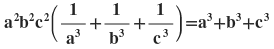
সমাধানঃ ধরি a:b = b:c = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ a = bk এবং b = ck
∴ a = (ck).k = ck2 এবং b = ck
বামপক্ষঃ
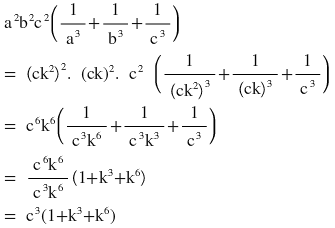
ডানপক্ষঃ
a3+b3+c3
= (ck2)3+(ck)3+c3
= c3k6+c3k3+c3
= c3(k6+k3+1)
∴ বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]
Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩
4(iii) যদি a:b = b:c হয় , তবে প্রমান করি যে ,
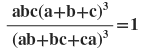
সমাধানঃ ধরি, a:b = b:c = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ a = bk এবং b = ck
আবার , a = (ck).k = ck2 , b = ck
বামপক্ষঃ
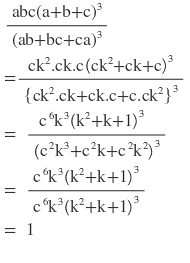
ডানপক্ষ =1
∴ বামপক্ষ =ডানপক্ষ [ প্রমাণিত ]
5(i) a,b,c,d ক্রমিক সমানুপাতী হলে প্রমান করি যে,
(a2+b2+c2)(b2+c2+d2) = (ab+bc+cd)2
সমাধানঃ
a,b,c,d ক্রমিক সমানুপাতী হলে,
a/b =b/c = c/d
ধরি , a/b =b/c = c/d = k [k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ a= bk , b=ck , c= dk
a = bk =(ck)k=ck2=(dk)k2 =dk3
b=ck=(dk)k =dk2
c =dk
বামপক্ষঃ
= (a2+b2+c2)(b2+c2+d2)
a,b এবং c এর মান বসিয়ে পাই ,
= {(dk3)2+(dk2)2+(dk)2}{(dk2)2+(dk)2+d2}
= (d2k6+d2k4+d2k2)(d2k4+d2k2+d2)
= d2k2(k4+k2+1) d2(k4+k2+1)
= d4k2(k4+k2+1)2
ডানপক্ষঃ
= (ab+bc+cd)2
a,b এবং c এর মান বসিয়ে পাই ,
= {(dk3)(dk2)+(dk2)(dk)+(dk)d}2
= (d2k5+d2k3+d2k)2
= d4k2(k4+k2+1)2
∴ বামপক্ষ = ডানপক্ষ [প্রমাণিত]
Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩
5(ii) a,b,c,d ক্রমিক সমানুপাতী হলে প্রমান করি যে,
(b-c)2+(c-a)2+(b-d)2 = (a-d)2
সমাধানঃ
a,b,c,d ক্রমিক সমানুপাতী হলে,
a/b =b/c = c/d
ধরি , a/b =b/c = c/d = k [k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ a= bk , b=ck , c= dk
a = bk =(ck)k=ck2=(dk)k2 =dk3
b=ck=(dk)k =dk2
c =dk
বামপক্ষঃ
(b-c)2+(c-a)2+(b-d)2
a,b এবং c এর মান বসিয়ে পাই ,
= (dk2-dk)2 + (dk-dk3)2+(dk2-d)2
= d2k2(k-1)2+d2k2(1-k2)2+d2(k2-1)2
= d2{k2(k2-2k+1)+k2(1-2k2+k4)+(k4-2k2+1)}
= d2(k4-2k3+k2+k2-2k4+k6+k4-2k2+1)
= d2 (k6-2k3+1)
= d2{(k3)2-2k3+1}
= d2(k3-1)2
ডানপক্ষঃ
(a-d)2
= {(dk3)-d}2
= d2(k3-1)2
∴ বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]
6(i) যদি m/a = n/b হয় , তবে দেখাই যে , (m2+n2)(a2+b2)=(am+bn)2
সমাধানঃ
m/a = n/b
ধরি , m/a = n/b = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
বা, m = ak এবং n = bk
বামপক্ষঃ
(m2+n2)(a2+b2)
m ও n এর মান বসিয়ে পাই,
= {(ak)2+(bk)2} (a2+b2)
= (a2k2+b2k2)(a2+b2)
= k2(a2+b2)(a2+b2)
= k2(a2+b2)2
ডানপক্ষঃ
(am+bn)2
m ও n এর মান বসিয়ে পাই,
= {a(ak)+b(bk)}2
= (a2k+b2k)2
= k2(a2+b2)2
∴ বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]
Madhyamik Math Solution Of Ratio And Proportion
6(ii) যদি a/b = x/y হয় , তবে দেখি যে , (a+b)(a2+b2)x3= (x+y)(x2+y2)a3
সমাধানঃ
a/b = x/y
বা, a/x = b/y
ধরি , a/x = b/y = k [ k(≠0) একটি আনুপাতিক ধ্রুবক ]
∴ a= xk , b =y k
বামপক্ষঃ
(a+b)(a2+b2)x3
a ও b এর মান বসিয়ে পাই,
= (xk+yk){(xk)2+(yk)2}x3
= k(x+y) (x2k2+y2k2) x3
= k(x+y) k2(x2+y2)x3
= k3x3(x+y)(x2+y2)
ডানপক্ষঃ
(x+y)(x2+y2)a3
a এর মান বসিয়ে পাই,
= (x+y)(x2+y2) (kx)3
= k3x3(x+y)(x2+y2)
∴ বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]
6(iii) x /(lm-n2) = y/(mn-l2) = z / (nl-m2) হয় , তবে দেখাই যে , lx+my+nz = 0
সমাধানঃ
ধরি ,x /(lm-n2) = y/(mn-l2) = z / (nl-m2) = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ x = k(lm-n2), y = k(mn-l2) এবং z= k(nl-m2)
এখন , lx-my+nz
x ,y এবং z এর মান বসিয়ে পাই,
= lk(lm-n2)+mk(mn-l2)+nk(nl-m2)
= kl2m-kln2+km2n-kml2+kn2l-knm2
= 0 [ প্রমানিত ]
6(iv) x / (b+c-a) = y/(c+a-b) = z / (a+b-c) হলে , দেখাই যে , (b-c)x+(c-a)y+(a-b)z=0
সমাধানঃ
x / (b+c-a) = y/(c+a-b) = z / (a+b-c) = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ x = k(b+c-a)
y = k(c+a-b)
z = k(a+b-c)
∴ (b-c)x+(c-a)y+(a-b)z
x ,y এবং z এর মান বসিয়ে পাই,
= k(b-c)(b+c-a) + k(c-a)(c+a-b)+k(a-b)(a+b-c)
= k(b2+bc-ba-cb-c2+ca)+k(c2+ca-cb-ac-a2+ab)+k(a2+ab-ac-ba-b2+bc)
= k(b2+bc-ba-cb-c2+ca+ c2+ca-cb-ac-a2+ab+ a2+ab-ac-ba-b2+bc)
= k ✕ (b2-b2+c2-c2+a2-a2+2bc-2bc+2ca-2ca+2ab-2ab)
= 0 [ প্রমাণিত ]
6(v) x/y = (a+2) / (a-2) হলে দেখাই যে , x2-y2 / x2+y2 = 4a / a2+4
সমাধানঃ
∴(x2-y2)/( x2+y2 )= 4a / (a2+4) [ প্রমাণিত ]
6(vi) x = 8ab /(a+b) হলে ,
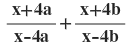
এর মাণ হিসাব করে লিখি ।
সমাধানঃ
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
7(i) a/3 = b/4 = c/ 7 হলে দেখাই যে , (a+b+c) /c = 2
সমাধানঃ
ধরি , a/3 = b/4 = c/ 7 = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ a = 3k , b = 4k এবং c = 7k
∴(a+b+c) /c
a,b এবং c এর মান বসিয়ে পাই,
= (3k+4k+7k)/7k
= 14k /7k
= 2 [ প্রমাণিত ]
7(ii) a/(q-r) = b/(r-p) = c / (p-q) হলে, দেখাইযে , a+b+c =0 = pa+qb+rc
সমাধানঃ
a/(q-r) = b/(r-p) = c / (p-q) = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ a = k(q-r)
b = k(r-p)
c = k(p-q)
∴ a+b+c
= k(q-r)+k(r-p)+k(p-q)
= k(q-r+r-p+p-q)
= k ✕ 0
= 0
আবার , pa+qb+rc
= pk(q-r)+qk(r-p)+rk(p-q)
= k(pq-pr+qr-pq+rp-pq)
= k ✕ 0
= 0
a+b+c =0 = pa+qb+rc [ প্রমাণিত ]
7(iii) (ax+by) /a = (bx-ay) / b হলে, দেখাই যে ,প্রতিটি অনুপাত x এর সমান ।
সমাধানঃ
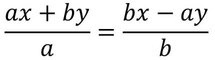
বা, abx +b2y = abx –a2y [ বজ্রগুনন করে পাই ]
বা, b2y+a2y =0
বা, y(b2+a2) = 0
এখন , (b2+a2) ≠ 0
∴ y = 0
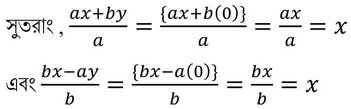
সুতরাং প্রতিটি অনুপাতের মাণ x এর সাথে সমান (প্রমাণিত )।
8(i) যদি (a+b) / (b+c) = (c+d) / (d+a) হয় , তবে প্রমান করি যে , c = a অথবা a+b+c+d = 0
সমাধানঃ
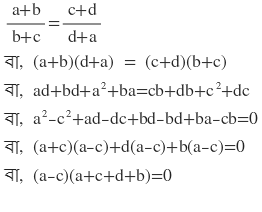
দুটি রাশির গুনফল শূন্য
∴ হয়, (a-c) =0
বা, a = c
অথবা,
(a+b+c+d) = 0
∴ a=c অথবা (a+b+c+d ) = 0 [ প্রমাণিত ]
Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩
গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
8(ii) যদি x / (b+c) = y / (c+a) = z / (a+b) হয় ,
তবে দেখাই যে , a / (y+z-x) = b / (z+x-y) = c / (x+y-z)
সমাধানঃ
ধরি , x / (b+c) = y / (c+a) = z / (a+b) = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ x = k(b+c) , y = k(c+a) এবং z = k (a+b)
প্রথমপক্ষঃ
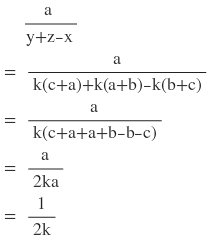
দ্বিতীয়পক্ষঃ
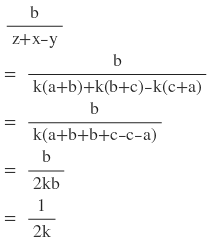
তৃতীয়পক্ষঃ
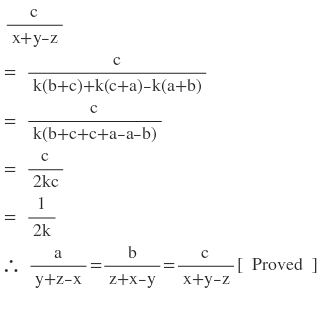
8(iii)
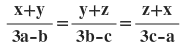
হলে্, দেখাই যে ,
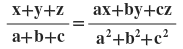
সমাধানঃ
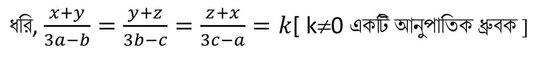
∴ x+y = k(3a-b)—(i)
(y+z) = k(3b-c)—(ii)
(z+x) = k(3c-a)—(iii)
(i),(ii) ও(iii) নং সমীকরণ যোগ করে পাই,
∴ x+y+y+z+z+x = k(3a-b)+k(3b-c)+k(3c-a)
বা, 2(x+y+z)= k(3a-b+3b-c+3c-a)
বা, 2(x+y+z)= k(2a+2b+2c)
বা, 2(x+y+z)= 2k(a+b+c)
বা, (x+y+z) = k(a+b+c)
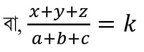
এখন , x = (x+y+z)-(y+z)
(x+y+z) এবং (y+z) -এর মান বসিয়ে পাই,
=k(a+b+c)-k(3b-c)
= k(a+b+c-3b+c)
= k(a-2b+2c)
y = (x+y+z)-(x+z)
(x+y+z)এবং (x+z)-এর মান বসিয়ে পাই,
= k(a+b+c)-k(3c-a)
= k(a+b+c-3c+a)
= k(b-2c+2a)
z = (x+y+z)-(x+y)
(x+y+z) এবং (x+y)-এর মান বসিয়ে পাই,
= k(a+b+c)-k(3a-b)
= k(a+b+c-3a+b)
= k(c-2a+2b)
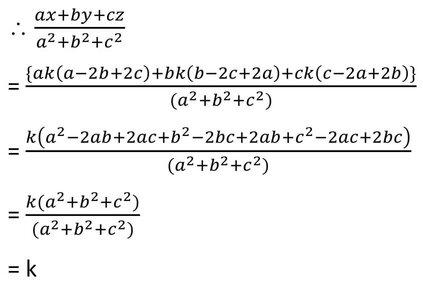
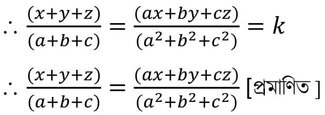
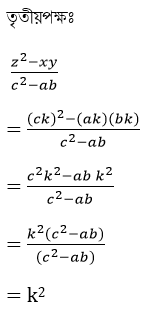
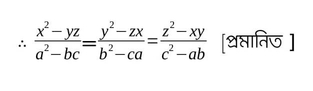
9(i) যদি ,
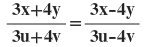
হয় , তবে দেখাই যে ,
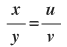
সমাধানঃ
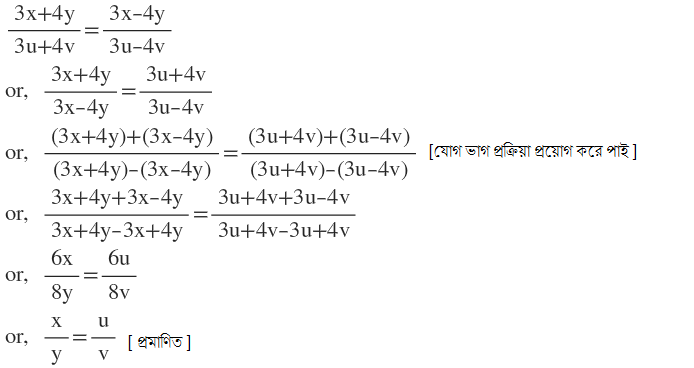
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
9(ii) (a+b+c+d) : (a+b-c-d) = (a-b+c-d) : (a-b-c+d) হলে , প্রমান করি যে , a:b = c:d
সমাধানঃ
| Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩ |
10(i)
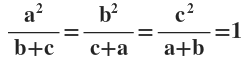
হলে , দেখাই যে ,
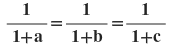
সমাধানঃ
10(ii) x2 : (by+cz) = y2 : (cz+ax) : z2 : (ax+by) =1 হলে , দেখাই যে ,
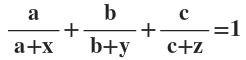
সমাধানঃ
x2 : (by+cz)=y2 : (cz+ax) = z2 : (ax+by) = 1
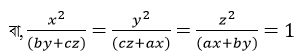
∴ x2 = (by+cz)
বা, x2+ax=by+cz+ax [উভয়পক্ষে ax যোগ করে পাই] ——(i)
আবার, y2+by=cz+ax+by [উভয়পক্ষে by যোগ করে পাই] ——(ii)
এবং z2 = ax+by
বা, z2+cz=ax+by+cz [উভয়পক্ষে cz যোগ করে পাই] ——(iii)
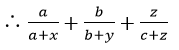
প্রথম রাশির লব ও হরকে x দ্বারা, দ্বিতীয় রাশির লব ও হরকে y দ্বারা এবং তৃতীয় রাশির লব ও হরকে z দ্বারা গুণ করে পাই,
Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩
11(i)
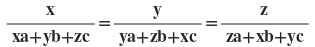
হলে , দেখাই যে , প্রতিটি অনুপাত 1 / (a+b+c) এর সাথে সমান ।
সমাধানঃ
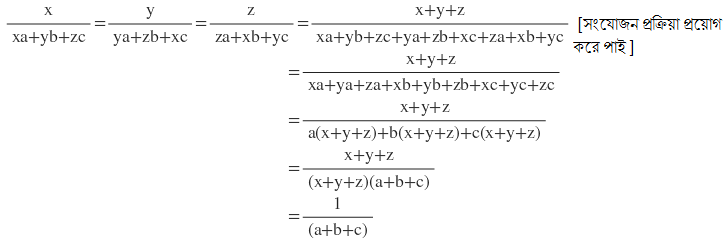
∴ প্রতিটি অনুপাতের মান 1/(a+b+c) এর সাথে সমান ।
Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩
11(ii) (x2-yz) / a = (y2-zx) / b = (z2-xy) /c হলে , প্রমান করো যে ,
(a+b+c)(x+y+z) = (ax+by+cz)
সমাধানঃ
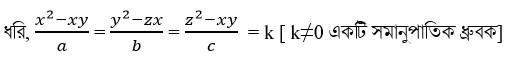
∴ x2-xy=ak —(i)
বা, x3-xyz=akx —-(ii) [উভয়কে x দ্বারা গুণ করে পাই]
y2-zx=bk —-(iii)
বা, y3-xyz=bky — (iv) [উভয়কে y দ্বারা গুণ করে পাই]
z2-xy=ck —-(v)
বা, z3-xyz=ckz — (vi) [উভয়কে z দ্বারা গুণ করে পাই]
(i) ,(iii) ও (v) নং সমীকরণ যোগ করে পাই ,
x2 –xy +y2-zx+z2-xy= ak+bk+ck
বা, x2+y2+z2 –xy-yz-zx = k(a+b+c) —-(vii)
(ii),(iv)এবং (vi) নং সমীকরণ যোগ করে পাই,
x3+y3+z3-3xyz= k(ax-by-cz)
বা, (x+y+z)(x2+y2+z2-xy-yz-zx)=k(ax+by+cz)
বা, (x+y+z)k(a+b+c)=k(ax+by+cz) [∵ x2+y2+z2 –xy-yz-zx = k(a+b+c) ]
বা, (x+y+z)(a+b+c)=(ax+by+cz)[যেহেতু k≠0 ,উভয়পক্ষে k দ্বারা ভাগ করে পাই ]
∴ (x+y+z)(a+b+c)=(ax+by+cz) [প্রমাণিত]
Koshe Dekhi 5.3 Class 10|অনুপাত সমানুপাত কষে দেখি ৫.৩
11(iii) a/ (y+z) = b /(z+x) = c / (x+y) হলে , প্রমান করি যে,
a(b-c) /(y2-z2) = b(c-a) / (z2-x2) = c(a-b) / (x2 –y2)
সমাধানঃ
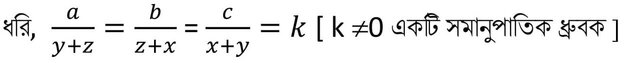
∴ a = k(y+z) এবং b = k(z+x) এবং c = k(x+y)
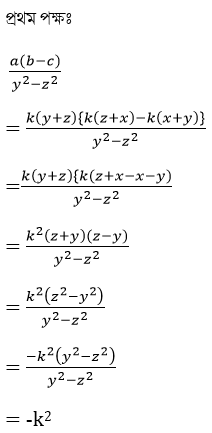
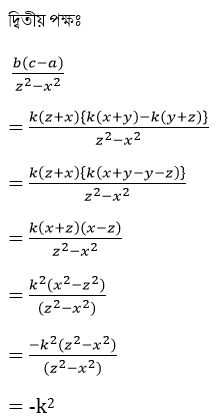
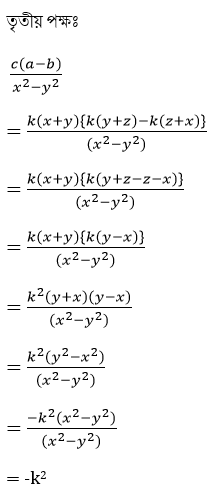
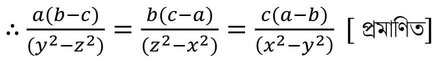
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
12. অতি সংক্ষিপ্ত প্রশ্ন (V.S.A)
A. বহু বিকল্পীয় প্রশ্ন (M.C.Q)
(i) 3 , 4 এবং 6 এর চতুর্থ সমানুপাতী
(a) 8
(b) 10
(c ) 12
(d) 24
Ans: (a) 8
সমাধানঃ ধরি 3,4 এবং 6 এর চতুর্থ সমানুপাতী হল x
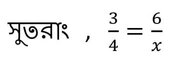
বা, 3x = 24
বা, x = 24/3
বা, x = 8
নির্ণেয় চতুর্থ সমানুপাতী হল 8 ।
(ii) 8 এবং 12 এর তৃতীয় সমানুপাতী
(a) 12
(b) 16
(c ) 18
(d) 20
Ans: (c ) 18
সমাধানঃ ধরি, 8 এবং 12 এর তৃতীয় সমানুপাতী হল x
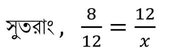
বা, 8x = 12✕12
বা, x = 144/8
বা, x = 18
∴ নির্ণেয় তৃতীয় সমানুপাতী হল 18
(iii) 16 এবং 25 এর মধ্যসমানুপাতী
(a) 400
(b) 100
(c ) 20
(d) 40
Ans: 20
সমাধানঃ ধরি , 16 এবং 25 এর মধ্যসমানুপাতী x
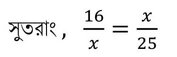
বা, x2 = 16✕25
বা , x = √16✕25
বা, x = 4✕5
বা , x = 20
∴ নির্ণেয় মধ্যসমানুপাতী হল 20
(iv) a একটি ধনাত্মক সংখ্যা এবং a : 27/64 = ¾ : a হলে, a এর মাণ কত ?
(a) 81/256
(b) 9
(c ) 9/16
(d) 16 / 9
Ans: (c ) 9/16
সমাধানঃ
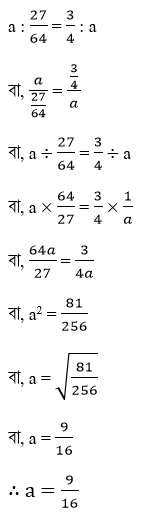
(v) 2a=3b=4c হলে, a:b:c হবে ,
(a) 3:4:6
(b) 4:3:6
(c) 3:6:4
(d) 6:4:3
Ans: (d) 6:4:3
সমাধানঃ ধরি , 2a=3b=4c=k [ k (≠ 0) একটি আনুপাতিক ধ্রুবক ]
∴ a = k/2
b = k/3
c = k/4
∴ a:b:c
=
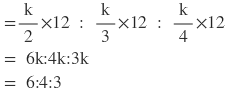
B. নীচের বিবৃতি গুলি সত্য না মিথ্যা লিখিঃ
(i) ab:c2 , bc:a2 এবং ca:b2 এর যৌগিক অনুপাত 1:1
Ans: সত্য
সমাধানঃ ab:c2 , bc:a2 এবং ca:b2 এর যৌগিক অনুপাত
= (ab)(bc)(ca) : a2b2c2
= a2b2c2 : a2b2c2
= 1 : 1
(ii) x3y , x2y2 এবং xy3 ক্রমিক সমানুপাতী
Ans: সত্য
সমাধানঃ
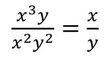
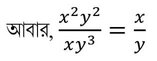
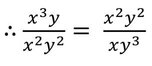
বা , x3y: x2y2 :: x2y2 : xy3
∴ x3y , x2y2 এবং xy3 ক্রমিক সমানুপাতী
(C ) শূন্যস্থান পূরণ করি ঃ
(i) তিনটি ক্রমিক সমানুপাতী ধনাত্মক সংখ্যার গুনফল 64 হলে , তাদের মধ্যসমানুপাতী ____________ ।
Ans: 4
সমাধানঃ ধরি , a ,b,c তিনটি ক্রমিক সমানুপাতী সংখ্যা ।
∴ a/b = b/c
বা, b2 = ac
বা, b3 = abc
বা, b3 = 64 [ যেহেতু তিনটি সংখ্যার গুনফল 64]
বা, b3 = 43
বা, b = 4
সুতরাং মধ্য সমানুপাতী হল 4 ।
(ii) a:2 = b:5 = c:8 হলে a এর 50% = b এর 20% = c এর ___________ ।
Ans: 12.5%
সমাধানঃ
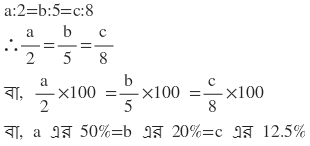
(iii) (x+2) এবং (x-3 ) এর মধ্য সমানুপাতী x হলে , x এর মাণ ___________ ।
Ans: -6
সমাধানঃ (x+2) এবং (x-3 ) এর মধ্য সমানুপাতী x
∴ (x+2):x :: x : (x-3)
বা, (x+2) / x = x / (x-3)
বা, x2 = (x+2)(x-3)
বা, x2 = x2+2x-3x-6
বা, x= -6
13. সংক্ষিপ্ত প্রশ্ন উত্তর (S.A):
(i) a/2 = b/3 = c/4 = (2a-3b+4c) / p হলে , p এর মাণ নির্ণয় করো ।
সমাধানঃ ধরি , a/2 = b/3 = c/4 = k [ k(≠ 0)একটি আনুপাতিক ধ্রুবক ]
∴ a =2k , b = 3k এবং c = 4k
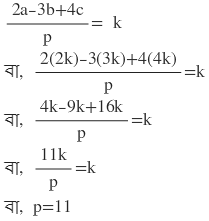
∴ p = 11
(ii) (3x-5y) : (3x+5y) = ½ হলে , (3x2-5y2) / (3x2+5y2) এর মাণ কত ?
সমাধানঃ
∴(3x2-5y2) / (3x2+5y2) = 7/8
(iii) a:b = 3:4 এবং x:y = 5:7 হলে, (3ax-by) : (4by -7ax ) কত নির্ণয় করি ।
সমাধানঃ
a:b = 3:4
ধরি , a = 3k , b= 4k [ k(≠0) একটি আনুপাতিক ধ্রুবক ]
আবার , x:y = 5:7
ধরি , x = 5m , y = 7m [m(≠0) একটি আনুপাতিক ধ্রুবক]
এখন , (3ax-by) : (4by -7ax )
= {3(3k)(5m)–(4k)(7m)} : {4(4k)(7m)-7(3k)(5m)} [∵ x = 5m , y = 7m]
= (45km-28km) : (112km : 105km)
= 17km : 7km
= 17:7
∴(3ax-by) : (4by -7ax ) = 17:7
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
(iv) x ,12 , y ,27 ক্রমিক সমানুপাতী হলে , x ও y এর ধনাত্মক মাণ নির্ণয় করি ।
সমাধানঃ x ,12 , y ,27 ক্রমিক সমানুপাতী
∴ x/12 =12/y = y/27
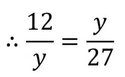
বা, y2 = 12✕27
বা, y2 = √324
বা, y = 18
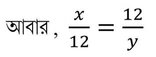
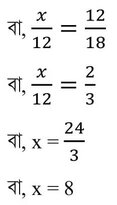
∴ x= 8 এবং y =18
(v) a:b = 3:2 এবং b:c = 3:2 হলে , (a+b) : (b+c) কত নির্ণয় করি ।
সমাধানঃ
a:b = 3:2 =9:6
b:c = 3:2=6:4
∴ a:b:c = 9:6:4
ধরি , a = 9k , b=6k এবং c = 4k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ a+b : b+c
= (9k+6k) : (6k+4k)
= 15k : 10k
= 3 : 2
∴ a+b : b+c =3:2
সম্পূর্ণ এই সমাধান PDF আকারে পেতে হলে নীচের বাটনে ক্লিক করুন ।
File Name- Koshe Dekhi 5.3 Class 10 [PDF] || অনুপাত সমানুপাত কষে দেখি ৫.৩
File Size- 6.13 Mb
Number of Pages-48
File Type- Hand Written Math Solutions
Important Links
আমাদের এই POST টি, আপনাদের পছন্দ হলে Share করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পাওয়ার জন্য আমাদের FACEBOOK PAGE টি LIKE করুন ,WhatsApp চ্যানেল জয়েন করুন এবং YouTube Channel Subscribe করুন ।