Ganit Prabha Class 8 Koshe Dekhi 6 Solution|পূরক কোণ,সম্পূরক কোণ ও সন্নিহিত কোণ কষে দেখি ৬ সমাধান|গণিত প্রভা অষ্টম শ্রেণি কষে দেখি ৬ সমাধান|গণিতপ্রভা ক্লাস ৮ কষে দেখি ৬ সমাধান|WBBSE Class Eight Chapter 6 Koshe Dekhi 6 Solution|West Bengal Board Class 8 Math Book Solution In Bengali
গণিতপ্রভা অষ্টম শ্রেণি সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
Ganit Prabha Class 8 Koshe Dekhi 6 Solution|পূরক কোণ,সম্পূরক কোণ ও সন্নিহিত কোণ কষে দেখি ৬ সমাধান|গণিত প্রভা অষ্টম শ্রেণি কষে দেখি ৬ সমাধান|গণিতপ্রভা ক্লাস ৮ কষে দেখি ৬ সমাধান|WBBSE Class Eight Chapter 6 Koshe Dekhi 6 Solution|West Bengal Board Class 8 Math Book Solution In Bengali
1.মনে মনে ভাবি ও লিখিঃ
(a) দুটি সূক্ষ্মকোণ পরস্পর পূরক হতে পারে কিনা লিখি ।
(b) দুটি সূক্ষ্মকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি ।
(c ) একটি সূক্ষ্মকোণ ও একটি স্থূলকোণ পরস্পর পূরক হতে পারে কিনা লিখি । দুটি সমকোণ পরস্পর পূরক হতে পারে কিনা লিখি ।
(d) দুটি স্থূলকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি ।
(e ) দুটি সমকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি ।
(f) একটি সূক্ষ্মকোণ ও একটি স্থূলকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি ।
(g) দুটি সন্নিহিত কোণ পরস্পর পূরক হতে পারে কিনা লিখি ।
(h) দুটি সন্নিহিত কোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি ।
সমাধানঃ
(a) দুটি সূক্ষ্মকোণ পরস্পর পূরক হতে পারে ।
উদাহরণঃ দুটি সূক্ষ্মকোণ 50° ও 40° এবং 50° +40° = 90°
(b) দুটি সূক্ষ্মকোণ পরস্পর সম্পূরক হতে পারে না ।
উদাহরণঃ দুটি সূক্ষ্মকোণ 80° ও 70° এবং 80° +70° = 150° ≠ 180°
(c) একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ পরস্পর পূরক হতে পারে না । দুটি সমকোণ পরস্পর পূরক হতে পারে না ।
উদাহরণঃ একটি সূক্ষ্মকোণ 20° ও একটি স্থূলকোণ 150° এবং 20° +150° = 170° ≠ 90°
আবার , 90° +90° = 180°≠ 90°
(d) দুটি স্থুলকোণ পরস্পর সম্পূরক হতে পারে না ।
উদাহরণঃ দুটি স্থূলকোণ যথাক্রমে 95° এবং 105° এবং 95° + 105° = 200° ≠ 180°
(e) দুটি সমকোণ পরস্পর সম্পূরক হতে পারে ।
উদাহরণঃ 90° +90° = 180°
(f) একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ পরস্পর সম্পূরক হতে পারে ।
উদাহরণঃ 140° +40° = 180°
(g) দুটি সন্নিহিত কোণ পরস্পর পূরক হতে পারে ।
(h) দুটি সন্নিহিত কোণ পরস্পর সম্পূরক হতে পারে ।
2. নীচের সন্নিহিত কোণগুলি আঁকি ও কোন কোণগুলি পরস্পর পূরক অথবা সম্পূরক লিখি :
45°, 45°; 120°, 30°; 70°, 110°; 42°, 48°; 37°, 43°; 85°, 95°;
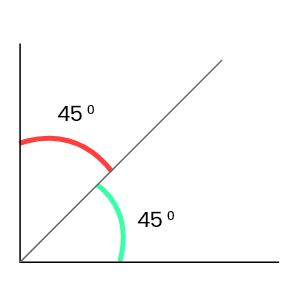
45°+45° = 90°
∴ 45° এবং 45° পরস্পর পূরক কোণ ।
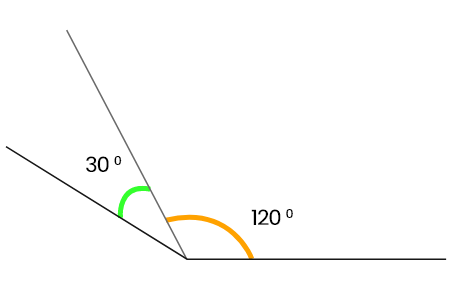
30° বা 120° পরস্পর পূরক বা সম্পূরক কোণ নয় ।
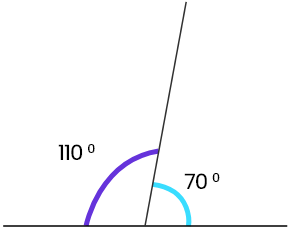
110°+70°= 180°
∴ 110° ও 70° পরস্পর সম্পূরক কোণ ।
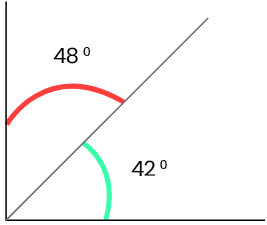
48°+42° =90°
∴ 48° এবং 42° পরস্পর পূরক কোণ।
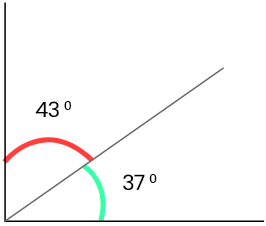
43° ও 37° পরস্পর পূরক বা সম্পূরক কোণ নয় ।
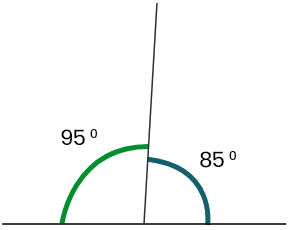
85° +95° = 180°
85° ও 95° কোণদুটি পরস্পর সম্পূরক কোণ ।
3. নীচের কোণগুলি দেখি ও কোন কোন কোণদুটি পরস্পর পূরক কোণ লিখি ;
31°, 47°, 64°, 29°, 43°, 59°, 17°, 26°
উত্তরঃ-
31° এর পূরক কোণ = 90° – 31° = 59°
47° এর পূরক কোণ = 90° – 47° = 43°
64° এর পূরক কোণ = 90° – 64° = 26°
29° এর পূরক কোণ = 90° – 29° = 61°
∴ পরস্পরের পূরক কোণগুলি –
(31°, 59°), (47°, 43°), (64°, 26°)
4. নীচের কোণগুলি দেখি ও কোন কোন কোণগুলি পরস্পর সম্পূরক কোণ লিখি :
47°, 58°, 69°, 75°, 133°, 105°, 122°, 125°
উত্তরঃ-
47° এর সম্পূরক কোণ = 180° – 47° = 133°
58° এর সম্পূরক কোণ = 180° – 58° = 122°
69° এর সম্পূরক কোণ = 180° – 69° = 111°
75° এর সম্পূরক কোণ = 180° – 75° = 105°
∴ পরস্পরের সম্পূরক কোণগুলি –
(47°, 133°), (58°, 122°), (75°, 105°)
5. সন্নিহিত কোণ কাকে বলে লিখি ও নীচের কোন কোণগুলি সন্নিহিত কোণ বুঝে লিখি :

উত্তরঃ- যখন দুটি কোণের শীর্ষবিন্দু একই ও কোণ দুটি একই সাধারণ বাহুর দুপাশে অবস্থিত হয় তখন ওই কোণ দুটিকে সন্নিহিত কোণ বলা হয়।
প্রশ্নের প্রথম, দ্বিতীয় ও তৃতীয় ছবি তিনটি সন্নিহিত কোণের ছবি। কারণ এই তিনটি ছবির প্রত্যেকটির শীর্ষবিন্দু এক এবং একই সাধারণ বাহুর দুপাশে অবস্থিত A ও B কোণ দুটি।
কিন্তু চতুর্থ ছবিটির কোণ দুটি সন্নিহিত কোণ নয়; কারণ A ও B কোণের শীর্ষবিন্দু পৃথক।
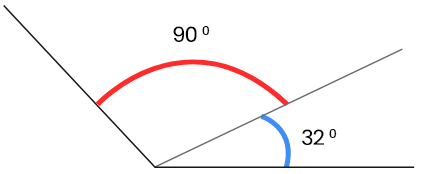
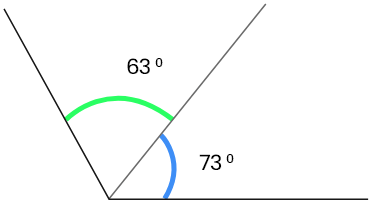
6. নিজে চাঁদার সাহায্যে সন্নিহিত কোণ আঁকি যার কোণদুটির মান হলো
35°, 45°; 18°, 42°; 32°,90°; 73°,63°
উত্তরঃ-
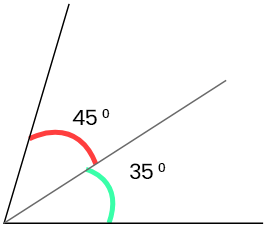
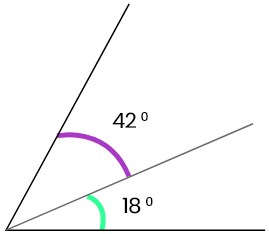
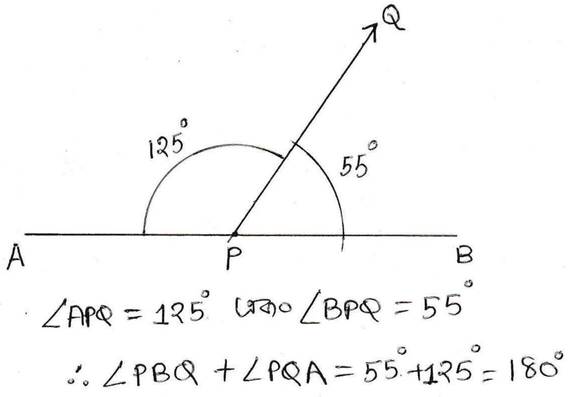
7. সায়ন্তনী একটি সরলরেখা AB আঁকল। আমি সেই সরলরেখার উপর কোনো বিন্দু P-তে অপর একটি রশ্মি PQ আঁকলাম। এর ফলে দুটি সন্নিহিত কোণ ∠BPQ ও ∠APQ তৈরি হলো । চাঁদার সাহায্যে মেপে ∠BPQ ও ∠APQ এর পরিমাপ লিখি ও ∠BPQ+∠APQ = কত লিখি ।
উত্তরঃ-
8. শাকিল দুটি সন্নিহিত কোণ ∠ABC ও ∠ABD আঁকল যাদের সমষ্টি 180°; আমিও শাকিলের মত ∠ABC ও ∠ABD এঁকে দেখি D, B ও C বিন্দু তিনটি একই সরলরেখায় আছে কিনা ।
উত্তরঃ-
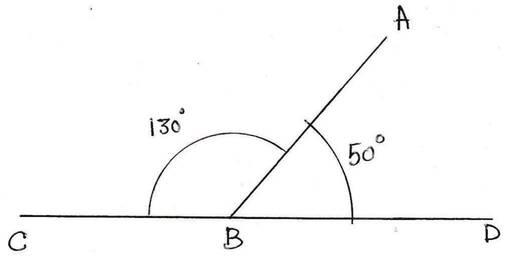
শাকিলের আঁকা দুটি সন্নিহিত কোণ ∠ABC ও ∠ABD এবং ∠ABC + ∠ABD =180°
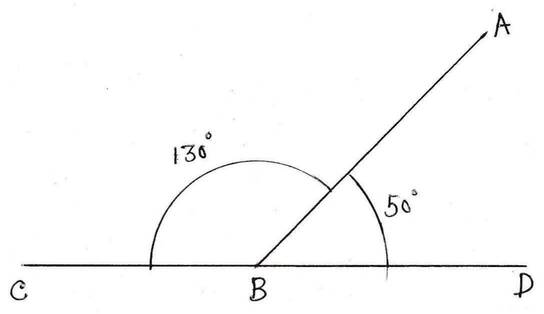
আমিও শাকিলের মত দুটি কোণ ∠ABC এবং ∠ABD আঁকলাম এবং দেখলাম যে D ,B এবং C একই সরলরেখায় অবস্থিত ।
9. ছবি থেকে x -এর মান নির্ণয় করি ।
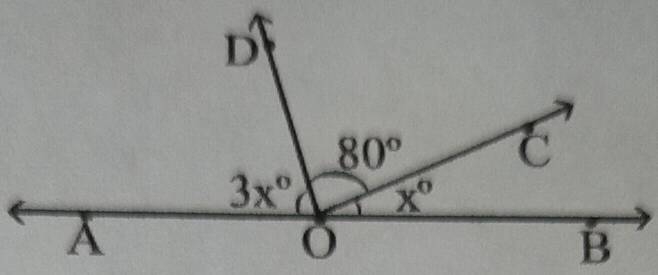
সমাধানঃ চিত্র থেকে পাই , ∠AOD =3x , ∠COD =80° এবং ∠BOC = x
যেহেতু , A ,O এবং B বিন্দুত্রয় একই সরলরেখায় অবস্থিত
∴ ∠AOD + ∠COD +∠BOC =180°
বা, 3x + 80° + x =180°
বা, 4x + 80° = 180°
বা, 4x = 180°-80°
বা, 4x = 100°
বা, x = 100°/4
বা, x = 25°
∴ x =25°
10. ছবিতে ∠AOP, ∠BOP -এর চেয়ে 140° বেশি । ∠AOP ও ∠BOP -এর মান নির্ণয় করি ।
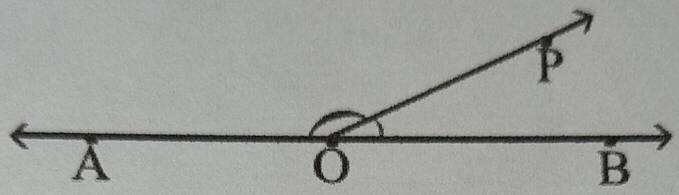
সমাধানঃ ∠AOP ,∠BOP –এর চেয়ে 140° বেশি
∴ ∠AOP = ∠BOP +140
চিত্র থেকে পাই ,
∠AOP + ∠BOP =180°
বা, ∠BOP+140 +∠BOP =180°
বা, 2∠BOP = 180°- 140°
বা, 2∠BOP =40°
বা, ∠BOP = 40°/2
বা, ∠BOP = 20°
∴ ∠AOP = ∠BOP +140° = 20°+140°=160°
11. দুটি সন্নিহিত কোণের মান 35° ও 145°; সন্নিহিত কোণের বহিঃস্থ বাহু দুটি কীভাবে অবস্থিত লিখি ।
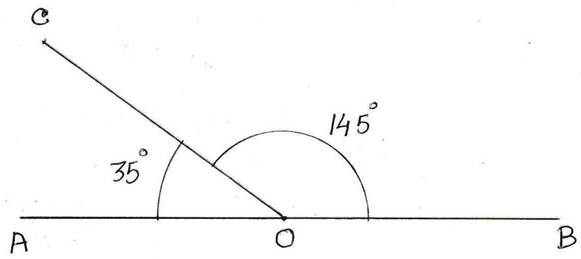
সমাধানঃ সন্নিহিত কোণ দুটির সমষ্টি 35° +145° = 180°
∴ দুটি সন্নিহিত কোণ 35° ও 145° একই সরলরেখায় অবস্থিত ।
12. ছবিতে OA ও OE কীভাবে অবস্থিত লিখি ।
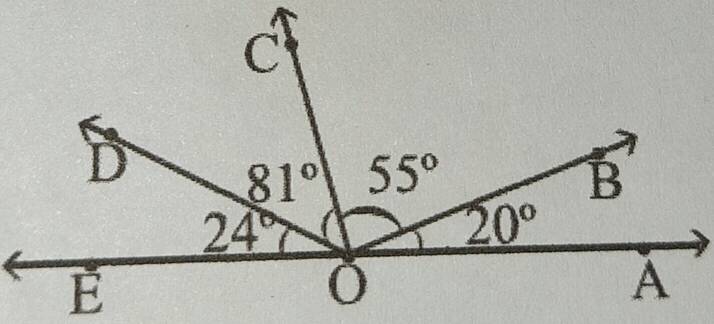
সমাধানঃ চিত্রে , ∠COA এবং ∠COE পরস্পর সন্নহিত কোণ ।
∠COA +∠COE
= ∠BOC + ∠AOB + ∠COD + ∠DOE
= 55° +20°+81°+24°
= 180°
∴ ∠COA এবং ∠COE সন্নিহিত কোণ দুটির সমষ্টি 180°
∴ OA এবং OE একই সরলরেখায় অবস্থিত ।
গণিতপ্রভা অষ্টম শ্রেণি সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
Really it is very helpful.
Realy it is very helpful web in exam time