Ganit Prabha Class 8 Koshe Dekhi 10.2 | ত্রৈরাশিক কষে দেখি ১০.২ সমাধান |গণিতপ্রভা অষ্টম শ্রেণী(ক্লাস 8)কষে দেখি ১০.২ সমাধান|WBBSE Class 8 Math Solution Of Chapter 10 Exercise 10.2 Solution.
Ganit Prabha Class 8 Koshe Dekhi 10.2|ত্রৈরাশিক কষে দেখি ১০.২ সমাধান|গণিতপ্রভা অষ্টম শ্রেণী(ক্লাস 8)কষে দেখি ১০.২ সমাধান|WBBSE Class 8 Math Solution Of Chapter 10 Exercise 10.2 Solution.
1. গ্রামের রাস্তা বাঁধানোর কাজ শুরু হবে। ঠিক হয়েছে 14 জন লোক দৈনিক 4 ঘণ্টা কাজ করে 15 দিনে সম্পূর্ণ কাজটি করতে পারবেন। কিন্তু 24 জন লোক দৈনিক 7 ঘণ্টা করে কাজ শুরু করলে কত দিনে কাজটি করবেন ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
উত্তরঃ–
গণিতের ভাষায় সমস্যাটি হল –
| লোকসংখ্যা (জন ) | দৈনিক কাজের সময় (ঘণ্টা ) | সময় (দিন ) |
| 14 | 4 | 15 |
| 24 | 7 | ? |
লোকসংখ্যা স্থির রেখে সময় বাড়ালে কাজের দিন কম লাগবে। সুতরাং, লোকসংখ্যা স্থির থাকলে সময়ের সাথে দিনসংখ্যার ব্যস্ত সমানুপাতী সম্পর্ক।
আবার , সময় স্থির রেখে লোকসংখ্যা বাড়ালে কাজের দিন কম লাগবে। সুতরাং, সময় স্থির থাকলে লোকসংখ্যার সাথে দিনসংখ্যার ব্যস্ত সমানুপাতী সম্পর্ক।

= 5 দিন
∴ 24 জন লোক দৈনিক 7 ঘণ্টা করে কাজ করলে কাজটি শেষ করতে সময় লাগবে 5 দিন ।
2. সুভাষ কাকার হাতে লেখা একটি 105 পৃষ্ঠার বইয়ের প্রতি পৃষ্ঠায় গড়ে 25টি করে লাইন আছে এবং প্রতি লাইনে গড়ে 8টি করে শব্দ আছে। এই বইটি যদি এমনভাবে ছাপাই যাতে প্রতি পৃষ্ঠায় 30 টি লাইন থাকবে এবং প্রতি লাইনে গড়ে 10টি করে শব্দ থাকবে, তবে সেই ছাপা বইটি কত পৃষ্ঠার বই হবে ত্রৈরাশিক পদ্ধতিতে হিসাব করে লিখি।
উত্তরঃ–
গণিতের ভাষায় সমস্যাটি হল –
| প্রতি পৃষ্ঠায় লাইনের সংখ্যা | প্রতি লাইনে শব্দের সংখ্যা | পৃষ্ঠার সংখ্যা |
| 25 | 8 | 105 |
| 30 | 10 | ? |
বইয়ের লাইন সংখ্যা স্থির রেখে শব্দ সংখ্যা বাড়ালে পৃষ্ঠা সংখ্যা কমবে। সুতরাং, শব্দ সংখ্যা ও পৃষ্ঠা সংখ্যার মধ্যে ব্যস্ত সমানুপাতী সম্পর্ক।
আবার , শব্দ সংখ্যা স্থির রেখে বইয়ের লাইন সংখ্যা বাড়ালে পৃষ্ঠা সংখ্যা কমবে। সুতরাং, বইয়ের লাইন সংখ্যা ও পৃষ্ঠা সংখ্যার মধ্যে ব্যস্ত সমানুপাতী সম্পর্ক।
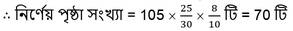
∴ প্রতি পৃষ্ঠায় 30টি লাইন থাকবে এবং প্রতি লাইনে গড়ে 10টি করে শব্দ থাকবে, তবে সেই ছাপা বইটি 70 পৃষ্ঠার হবে ।
Ganit Prabha Class 8 Koshe Dekhi 10.2|ত্রৈরাশিক কষে দেখি ১০.২ সমাধান
3. একটি কৃষি খামারের 540 বিঘা জমি 14 দিনে চাষ করতে হবে। প্রথম 4 দিনে সমক্ষমতা সম্পন্ন 5টি ট্রাক্টর 120 বিঘা জমি চাষ করল। সময়মতো চাষের কাজ শেষ করতে হলে আর কটি ট্রাক্টর লাগবে ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
উত্তরঃ–
গণিতের ভাষায় সমস্যাটি হল –
| জমির পরিমাণ (বিঘা ) | দিনসংখ্যা | ট্রাক্টরের সংখ্যা |
| 120 | 4 | 5 |
| 540 -120 = 420 | 14- 4 = 10 | ? |
জমির পরিমাণ স্থির রেখে সময় বাড়ালে ট্রাক্টর কম লাগবে। সুতরাং, সময় ও ট্রাক্টর সংখ্যার মধ্যে ব্যস্ত সমানুপাতী সম্পর্ক।
আবার , সময় স্থির রেখে জমির পরিমাণ বাড়ালে ট্রাক্টর বেশি লাগবে। সুতরাং, জমির পরিমাণ ও ট্রাক্টর সংখ্যার মধ্যে সরল সমানুপাতী সম্পর্ক।
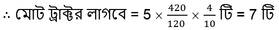
∴ নির্ণেয় ট্রাক্টরের সংখ্যা 7 টি ।
∴ সময় মত কাজটি শেষ করতে হলে আরও (7-5) টি = 2 টি ট্রাক্টর লাগবে ।
Ganit Prabha Class 8 Koshe Dekhi 10.2|ত্রৈরাশিক কষে দেখি ১০.২ সমাধান
4. 30 জন লোক 15 দিনে একটি গ্রামের রাস্তার অংশ সারান। যদি আরও 10 জন লোক কাজটি করতে আসেন তাহলে রাস্তাটির বাকি অংশ সারাতে কত দিন লাগবে ত্রৈরাশিক পদ্ধতিতে হিসাব করি ।
উত্তরঃ–
গণিতের ভাষায় সমস্যাটি হল –
| লোকসংখ্যা (জন ) | কাজের পরিমাণ | সময় (দিন ) |
| 30 | 3/7 | 15 |
| 30+10 = 40 | 1-3/7 =4/7 | ? |
লোকসংখ্যা স্থির রেখে কাজ বাড়ালে সময় বেশি লাগবে। সুতরাং, লোকসংখ্যা ও সময়ের মধ্যে সরল সমানুপাতী সম্পর্ক।
আবার , কাজ স্থির রেখে লোকসংখ্যা বাড়ালে সময় কম লাগবে। সুতরাং, লোকসংখ্যা ও সময়ের মধ্যে ব্যস্ত সমানুপাতী সম্পর্ক।
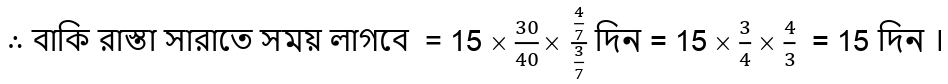
∴ রাস্তাটির বাকি অংশ সারাতে সময় লাগবে 15 দিন ।
5. 5 অশ্বক্ষমতা সম্পন্ন একটি পাম্প 36000 লিটার জল 8 ঘণ্টায় উপরে তুলতে পারে। 7 অশ্বক্ষমতা সম্পন্ন পাম্পের 63000 লিটার জল তুলতে কত সময় লাগবে ত্রৈরাশিক পদ্ধতিতে হিসাব করি ।
উত্তরঃ–
গণিতের ভাষায় সমস্যাটি হল –
| পাম্পের ক্ষমতা (অশ্বক্ষমতা) | জলের পরিমাণ (লিটার ) | সময় ( ঘন্টা ) |
| 5 | 36000 | 8 |
| 7 | 63000 | ? |
পাম্পের ক্ষমতা স্থির রেখে জলের পরিমাণ বাড়ালে সময় বেশি লাগবে। সুতরাং, জলের পরিমাণ ও সময়ের মধ্যে সরল সমানুপাতী সম্পর্ক।
আবার , জলের পরিমাণ স্থির রেখে পাম্পের ক্ষমতা বাড়ালে সময় কম লাগবে। সুতরাং, পাম্পের ক্ষমতা ও সময়ের মধ্যে ব্যস্ত সমানুপাতী সম্পর্ক।
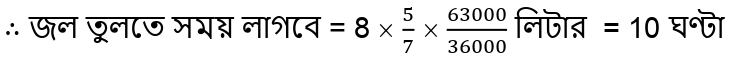
∴ 7 অশ্বক্ষমতা সম্পন্ন পাম্পের 63000 লিটার জল তুলতে 10 ঘণ্টা সময় লাগবে ।
Ganit Prabha Class 8 Koshe Dekhi 10.2|ত্রৈরাশিক কষে দেখি ১০.২ সমাধান
6. একটি কারখানায় 5 অশ্বক্ষমতা ও 3 অশ্বক্ষমতার দুটি মোটর আছে। 5 অশ্বক্ষমতার মোটরটি 8 ঘণ্টা চালালে 20 একক বিদ্যুৎ খরচ হয়। 3 অশ্বক্ষমতার মোটরটি 10 ঘণ্টা চালালে কত একক বিদ্যুৎ খরচ হবে ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
উত্তরঃ–
গণিতের ভাষায় সমস্যাটি হল –
| মোটোরের ক্ষমতা (অশ্ব ক্ষমতা ) | সময় (ঘণ্টা ) | বিদ্যুৎ খরচের পরিমাণ |
| 5 | 8 | 20 |
| 3 | 10 | ? |
মোটরের শক্তি স্থির রেখে সময় বাড়ালে বিদ্যুৎ খরচ বেশি লাগবে। সুতরাং, সময় ও বিদ্যুৎ খরচের মধ্যে সরল সমানুপাতী সম্পর্ক।
আবার , সময় স্থির রেখে মোটরের শক্তি বাড়ালে বিদ্যুৎ খরচ বেশি লাগবে। সুতরাং, মোটরের শক্তি ও বিদ্যুৎ খরচের মধ্যে সরল সমানুপাতী সম্পর্ক।
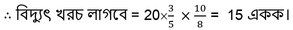
∴ 3 অশ্বক্ষমতার মোটরটি 10 ঘণ্টা চালালে 15 একক বিদ্যুৎ খরচ হবে ।
Ganit Prabha Class 8 Koshe Dekhi 10.2|ত্রৈরাশিক কষে দেখি ১০.২ সমাধান
7. গোপালনগরের একটি তাঁত কারখানায় 14 জন তাঁতি 12 দিনে 210 টি শাড়ি বুনতে পারেন। পুজার সময়ে 10 দিনের মধ্যে 300 টি শাড়ি যোগান দেওয়ার অর্ডার এলো। সময় মতো সেই শাড়ি যোগান দিতে হলে আরও কত জন তাঁতি নিয়োগ করতে হবে ব্যাপকতর ত্রৈরাশিক পদ্ধতিতে হিসাব করে লিখি।
উত্তরঃ–
গণিতের ভাষায় সমস্যাটি হল –
| শাড়ির সংখ্যা (টি ) | সময় (দিন ) | তাঁতির সংখ্যা (জন ) |
| 210 | 12 | 14 |
| 300 | 10 | ? |
শাড়ি সংখ্যা স্থির রেখে সময় বাড়ালে তাঁতি কম লাগবে। সুতরাং, সময় ও তাঁতির মধ্যে ব্যস্ত সমানুপাতী সম্পর্ক।
আবার , সময় স্থির রেখে শাড়ি সংখ্যা বাড়ালে তাঁতি বেশি লাগবে। সুতরাং, শাড়ি সংখ্যা ও তাঁতির মধ্যে সরল সমানুপাতী সম্পর্ক।
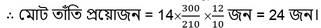
সুতরাং, সময় মতো শাড়ির যোগান দিতে হলে আরও (24 – 14) জন = 10 জন তাঁতি নিয়োগ করতে হবে।
Ganit Prabha Class 8 Koshe Dekhi 10.2|ত্রৈরাশিক কষে দেখি ১০.২ সমাধান
8. একটি সংস্থা জাহাজ থেকে 10 দিনে জাহাজের মাল নামানোর বরাত পেয়েছে। সংস্থাটি তার জন্য 280 জন লোক নিয়োগ করেছে। 3 দিন পরে দেখা গেল কাজটির ¼ অংশ সম্পূর্ণ হয়েছে। আর কত জন লোক নিয়োগ করলে কাজটি সময় মতো শেষ হবে তা ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
উত্তরঃ–
গণিতের ভাষায় সমস্যাটি হল –
| সময় (দিন) | কাজের পরিমাণ (অংশে ) | লোকসংখ্যা (জন ) |
| 3 | ¼ | 280 |
| 10-3 = 7 | 1- ¼ = ¾ | ? |
সময় স্থির রেখে কাজের পরিমাণ বাড়ালে লোকসংখ্যা বেশি লাগবে। সুতরাং, কাজের পরিমাণ ও লোকসংখ্যার মধ্যে সরল সমানুপাতী সম্পর্ক।
আবার , কাজের পরিমাণ স্থির রেখে সময় বাড়ালে লোকসংখ্যা কম লাগবে। সুতরাং, সময় ও লোকসংখ্যার মধ্যে ব্যস্ত সমানুপাতী সম্পর্ক।
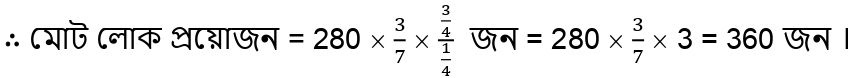
∴ সময়মতো কাজ শেষ করতে হলে আরও (360 – 280) জন = 80 জন লোক নিয়োগ করতে হবে।
Ganit Prabha Class 8 Koshe Dekhi 10.2|ত্রৈরাশিক কষে দেখি ১০.২ সমাধান
গণিতপ্রভা অষ্টম শ্রেণী বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
9. একটি যন্ত্রচালিত তাঁতের ক্ষমতা একটি হস্তচালিত তাঁতের খমতার 2¼ গুন। টি হস্তচালিত তাঁত 1080 মিটার দৈর্ঘ্যের কাপড় 18 দিনে তৈরি করে। 2700 মিটার দৈর্ঘ্যের কাপড় 15 দিনে তৈরি করতে কত গুলি যন্ত্র চালিত তাঁত লাগবে তা ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
উত্তরঃ–
গণিতের ভাষায় সমস্যাটি হল –
| কাপড়ের দৈর্ঘ্য (মিটারে ) | সময় (দিন ) | হস্তচালিত তাঁতের সংখ্যা |
| 1080 | 18 | 12 |
| 2700 | 15 | ? |
কাপড়ের পরিমাণ স্থির রেখে সময় বাড়ালে হস্তচালিত তাঁত কম লাগবে। সুতরাং, সময় ও হস্তচালিত তাঁতের মধ্যে ব্যস্ত সমানুপাতী সম্পর্ক।
আবার , সময় স্থির রেখে কাপড়ের পরিমাণ বাড়ালে হস্তচালিত তাঁত বেশি লাগবে। সুতরাং, শাড়ি সংখ্যা ও হস্তচালিত তাঁতের মধ্যে সরল সমানুপাতী সম্পর্ক।

= 16 টি যন্ত্রচালিত তাঁতের কাজ
∴ নির্ণেয় যন্ত্রচালিত তাঁতের সংখ্যা 16 টি ।
Ganit Prabha Class 8 Koshe Dekhi 10.2|ত্রৈরাশিক কষে দেখি ১০.২ সমাধান
10. 25 জন কৃষক একটি সমবায় সমিতির 2400 বিঘা জমি 36 দিনে চাষ করেন। সমিতি একটি ট্রাক্টর কেনায় দেখা যায় অর্ধেক জমি 30 দিনে চাষ করা যায়। একটি ট্রাক্টরের ক্ষমতা কত জন কৃষকের চাষ করার খমতার সমান তা ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
উত্তরঃ–
গণিতের ভাষায় সমস্যাটি হল –
| জমির পরিমাণ (বিঘা ) | সময় (দিন ) | কৃষকের সংখ্যা (জন ) |
| 2400 | 36 | 25 |
| 2400/2 = 1200 | 30 | ? |
চাষের জমির পরিমাণ স্থির রেখে সময় বাড়ালে কৃষক কম লাগবে। সুতরাং, সময় ও কৃষকের মধ্যে ব্যস্ত সমানুপাতী সম্পর্ক।
আবার , সময় স্থির রেখে চাষের জমির পরিমাণ বাড়ালে কৃষক বেশি লাগবে। সুতরাং, চাষের জমির পরিমাণ ও কৃষকের মধ্যে সরল সমানুপাতী সম্পর্ক।
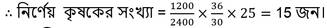
∴ একটি ট্রাক্টরের ক্ষমতা 15 জন কৃষকের চাষ করার ক্ষমতার সমান।
Ganit Prabha Class 8 Koshe Dekhi 10.2|ত্রৈরাশিক কষে দেখি ১০.২ সমাধান
11. একটি জাহাজের কলকাতা থেকে কোচিন যেতে 25দিন সময় লাগে। জাহাজ্টি 36 জন নাবিকসহ এবং প্রত্যেক নাবিকের জন্য প্রতিদিন 850 গ্রাম খাবারের ব্যবস্থা করে যাত্রা শুরু করল । কিন্তু 13 দিন পরে ওই জাহাজটি অপর একটি ডুবন্ত জাহাজ থেকে 15 জন নাবিককে উদ্ধার করল এবং জাহাজটির গতিবেগ বাড়িয়ে দিয়ে 10 দিনে কোচিন পৌঁছাল। এখন প্রত্যেক নাবিক প্রতিদিন কতটা পরিমান খাবার খেলে ওই মজুত খাবারে তারা কোচিন নিরাপদে পৌঁছাতে পারবে এবং সমস্ত খাবার ওই সময়ে শেষ হয়ে যাবে। ত্রৈরাশিক পদ্ধতিতে হিসাব করি ।
উত্তরঃ–
13 দিন পর খাবার অবশিষ্ট ছিল=(25 – 13 ) দিনের = 12 দিনের
13 দিন পর মোট নাবিক সংখ্যা=( 36 + 15) জন = 51 জন
গণিতের ভাষায় সমস্যাটি হল –
| নাবিকের সংখ্যা | সময় (দিন ) | দৈনিক খাবারের পরিমাণ (গ্রাম ) |
| 36 | 12 | 850 |
| 51 | 10 | ? |
নাবিক সংখ্যা স্থির রেখে সময় বাড়ালে খাদ্যের পরিমাণ কমবে। সুতরাং, সময় ও খাদ্যের মধ্যে ব্যস্ত সমানুপাতী সম্পর্ক।
আবার , সময় স্থির রেখে নাবিক সংখ্যা বাড়ালে খাদ্যের পরিমাণ কমবে। সুতরাং, নাবিক সংখ্যা ও খাদ্যের মধ্যে ব্যস্ত সমানুপাতী সম্পর্ক।
∴ প্রতিদিন প্রত্যেক নাবিকের খাদ্য প্রয়োজন=850☓ 36 /51 ☓ 12/10 গ্রাম = 720 গ্রাম ।
Ganit Prabha Class 8 Koshe Dekhi 10.2|ত্রৈরাশিক কষে দেখি ১০.২ সমাধান
12. একটি গ্রামে 36 জন লোক প্রতিদিন 6 ঘণ্টা কাজ করে 8 দিনে 120 মিটার রাস্তা তৈরি করতে পারেন। আরও 6 জন লোক কাজটির সাথে যুক্ত হলো এবং দৈনিক কাজের পরিমান আরও 2 ঘণ্টা করে বাড়ানো হলো। এখন 9 দিনে কত দৈর্ঘ্যের রাস্তা তৈরি করা যাবে তা ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
উত্তরঃ–
গণিতের ভাষায় সমস্যাটি হল –
| লোকসংখ্যা (জন ) | দৈনিক কাজের সময় (ঘণ্টা ) | সময় (দিন ) | রাস্তার দৈর্ঘ্য (মিটার ) |
| 36 | 6 | 8 | 120 |
| 36+6 = 42 | 6+2 = 8 | 9 | ? |
লোক সংখ্যা স্থির রেখে সময় বাড়ালে রাস্তার পরিমাণ বাড়বে। সুতরাং, সময় ও রাস্তার মধ্যে সরল সমানুপাতী সম্পর্ক।
আবার , সময় স্থির রেখে লোক সংখ্যা বাড়ালে রাস্তার পরিমাণ বাড়বে। সুতরাং, লোক সংখ্যা ও রাস্তার মধ্যে সরল সমানুপাতী সম্পর্ক।
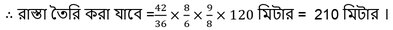
∴ এখন 9 দিনে 210 মিটার রাস্তা তৈরি করা যাবে ।
13. 250 জন লোক 50 মিটার দীর্ঘ, 35 মিটার প্রশস্ত এবং 5.2 মিটার গভীর একটি পুকুর প্রতিদিন 10 ঘণ্টা কাজ করে 18 দিনে কাটতে পারেন। 65 মিটার দীর্ঘ, 40 মিটার প্রশস্ত এবং 5.6 মিটার গভীর অপর একটি পুকুর 300 জন লোক প্রতিদিন 8 ঘণ্টা কাজ করে কত দিনে কাটতে পারবেন তা ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
উত্তরঃ–
গণিতের ভাষায় সমস্যাটি হল –
| লোকসংখ্যা (জন ) | পুকুরের আয়তন (ঘনমি. ) | দৈনিক কাজের সময় (ঘন্টা ) | সময় (দিন ) |
| 250 | 50☓35☓5.2 | 10 | 120 |
| 300 | 65☓40☓5.6 | 8 | ? |
লোক সংখ্যা স্থির রেখে পুকুরের আয়তন বাড়ালে সময়ের পরিমাণ বাড়বে। সুতরাং, পুকুরের আয়তন ও সময়ের মধ্যে সরল সমানুপাতী সম্পর্ক।
আবার , পুকুরের আয়তন স্থির রেখে লোক সংখ্যা বাড়ালে সময়ের পরিমাণ কমবে। সুতরাং, লোক সংখ্যা ও সময়ের মধ্যে ব্যস্ত সমানুপাতী সম্পর্ক।
∴ দ্বিতীয় পুকুরটি কাটতে সময় লাগবে

∴ প্রতিদিন 8 ঘণ্টা কাজ করে 30 দিনে পুকুরটি কাটতে পারবেন ।
14. নীচের পারস্পরিক সম্পর্কগুলি দেখে গণিতের গল্প তৈরি করি ও ত্রৈরাশিক পদ্ধতিতে উত্তর খুঁজি।
(a)
| ক্ষমতা (অশ্বশক্তি ) | সময় (ঘন্টা ) | বিদ্যুৎ খরচ ( ইউনিট ) |
| 5 | 8 | 20 |
| 3 | 10 | ? |
উত্তরঃ–
গনিতের গল্প – 5 অশ্বশক্তি ক্ষমতা সম্পন্ন মোটর দৈনিক 8 ঘণ্টা চললে 20 ইউনিট বিদ্যুৎ খরচ হয়। তাহলে 3 অশ্বশক্তি ক্ষমতা সম্পন্ন একটি মোটর দৈনিক 10 ঘণ্টা চললে কত ইউনিট বিদ্যুৎ খরচ হবে?
| ক্ষমতা (অশ্বশক্তি ) | সময় (ঘন্টা ) | বিদ্যুৎ খরচ ( ইউনিট ) |
| 5 | 8 | 20 |
| 3 | 10 | ? |
ক্ষমতা স্থির রেখে সময় বাড়ালে বিদ্যুৎ খরচ বাড়বে। সুতরাং, সময় ও বিদ্যুৎ খরচের মধ্যে সরল সমানুপাতী সম্পর্ক।
আবার , সময় স্থির রেখে ক্ষমতা বাড়ালে বিদ্যুৎ খরচ বাড়বে। সুতরাং, ক্ষমতা ও বিদ্যুৎ খরচের মধ্যে সরল সমানুপাতী সম্পর্ক।
∴ বিদ্যুৎ খরচ হবে = (20☓ 3/ 5 ☓ 10/8) ইউনিট = 15 ইউনিট
(b)
| ক্ষেত মজুরের সংখ্যা (জন ) | সময় (দিন ) | জমির পরিমাণ (বিঘা ) |
| 5 | 15 | 18 |
| 10 | 10 | ? |
উত্তরঃ–
গনিতের গল্প – 5 জন খেতমজুর 15 দিনে 18 বিঘা জমি চাষ করতে পারে। তাহলে 10 জন খেতমজুর 10 দিনে কত বিঘা জমি চাষ করতে পারবে?
| ক্ষেত মজুরের সংখ্যা (জন ) | সময় (দিন ) | জমির পরিমাণ (বিঘা ) |
| 5 | 15 | 18 |
| 10 | 10 | ? |
ক্ষেতমজুরের সংখ্যা স্থির রেখে সময় বাড়ালে জমি চাষের পরিমাণ বাড়বে। সুতরাং, সময় ও জমি চাষের পরিমাণের মধ্যে সরল সমানুপাতী সম্পর্ক।
আবার , সময় স্থির রেখে ক্ষেতমজুরের সংখ্যা বাড়ালে জমি চাষের পরিমাণ বাড়বে। সুতরাং, ক্ষেতমজুরের সংখ্যা ও জমি চাষের পরিমাণের মধ্যে সরল সমানুপাতী সম্পর্ক।
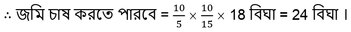
∴ 10 জন ক্ষেত মজুর 10 দিনে 24 বিঘা জমি চাষ করতে পারবে ।
গণিতপ্রভা অষ্টম শ্রেণী বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন